Глава 3. Решение уравнений и неравенств
3.3.
3.3.1.
Если поставлена задача найти такие числа  которые удовлетворяли бы сразу всем n уравнениям
которые удовлетворяли бы сразу всем n уравнениям
и обращали бы их в верные числовые равенства, то говорят, что задана система из n уравнений с n неизвестными. В школьной практике, как правило, встречаются системы с двумя и тремя неизвестными, хотя, разумеется, бывают и исключения.
Наиболее распространённым методом решения этих систем является метод последовательного исключения неизвестных (метод Гаусса), который для линейных функций 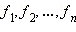 может быть представлен в виде алгоритма, являющегося наиболее общим.
может быть представлен в виде алгоритма, являющегося наиболее общим.
Метод Гаусса для решения системы линейных уравнений
- Выражаем первое неизвестное из первого уравнения и подставляем его в остальные уравнения.
- Получаем новую систему, в которой число уравнений и неизвестных на 1 меньше.
- С новой системой поступаем таким же образом и так продолжаем до тех пор, пока не останется одно линейное уравнение, которое легко решается.
- Когда получено значение последнего неизвестного xn, подставляем его в уравнение, которое позволяет найти xn – 1 по xn.
- По найденным xn – 1 и xn находим xn – 2 и таким образом находим последовательно все неизвестные.
Для систем нелинейных уравнений этот метод не всегда применим уже в силу того, что из уравнений системы совсем не обязательно можно будет выразить одну неизвестную через остальные.
Пример 1Решить систему уравнений
Выразим из первого уравнения переменную x: 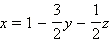 и подставим её во второе и третье уравнения:
и подставим её во второе и третье уравнения:
Выразим теперь из второго уравнения переменную 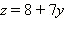 и подставим её в третье уравнение системы:
и подставим её в третье уравнение системы:
Теперь третье уравнение зависит только от y и мы можем его решить:
Итак, переменная y найдена. По уже полученным формулам для x и z мы можем последовательно их найти: 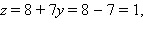
Ответ. (2; –1; 1).
|
Этот метод иногда можно применить и для решения нелинейных систем.
Пример 2Решить систему уравнений
Выразим z из второго уравнения: z = 1 + 2x – y и подставим его в первое и третье уравнения. Получим систему из двух уравнений с двумя неизвестными:
Опять из первого уравнения выражаем y (её легче выразить, чем x): 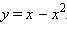 Подставляем y во второе уравнение и получаем:
Подставляем y во второе уравнение и получаем:
Теперь по найденному x находим y и z:
Ответ. (1; 0; 3), (–1; –2; 1).
|






 которые удовлетворяли бы сразу всем
которые удовлетворяли бы сразу всем 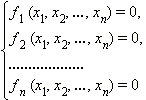
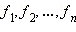 может быть представлен в виде алгоритма, являющегося наиболее общим.
может быть представлен в виде алгоритма, являющегося наиболее общим.



