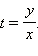Ни одно из уравнений системы не является однородным, однако в левой части уравнений стоят однородные функции. Применим стандартный приём, который позволяет свести систему такого вида к однородному уравнению. Умножим первое уравнение на 4, а второе на 3 и вычтем из первого уравнения второе. Имеем:
А это уравнение уже однородное. Очевидно, что пара (0; 0) является его решением, однако непосредственной подстановкой можно убедиться, что эта пара не является решением исходной системы уравнений. Значит, разделим уравнение на
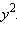
Получим:
Стандартная замена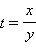 
приводит нас к квадратному уравнению 
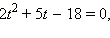корни которого 
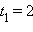и 
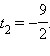Система распалась на две:
1) 
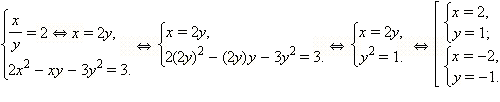
2) 
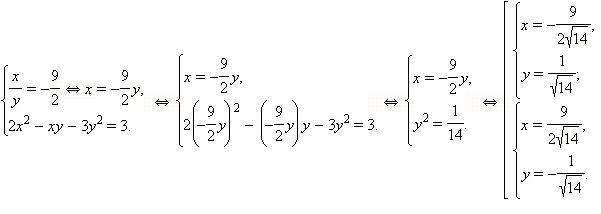
Ответ.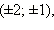 
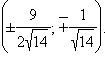
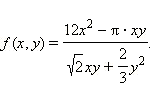
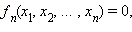где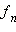 
– однородные функции, то, во-первых, нужно проверить, существуют не является ли решением 
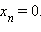После того, как установлено отсутствие таких решений (или же все такие решения найдены), вводится стандартная замена переменных 
называется 
однородной.
Имеем
