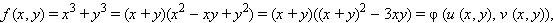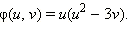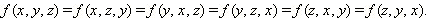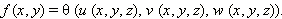Глава 3. Решение уравнений и неравенств
3.3.
3.3.3.
Пример 1Многочлен от двух переменных вида 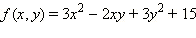 является симметрической функцией. В самом деле,
является симметрической функцией. В самом деле,
Пример 2Функция 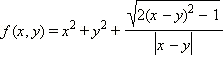 является симметрической. В самом деле,
является симметрической. В самом деле,
Оказывается, справедлива замечательная теорема о симметрических многочленах.
Теорема 1.
(о симметрических многочленах) Любой симметрический многочлен от двух переменных представим в виде функции от двух основных симметрических многочленов
 |
Другими словами, для любого симметрического многочлена f (x, y) существует такая функция двух переменных φ (u, v), что
Доказательство этого факта хотя и доступно школьнику, но далеко выходит за рамки школьного курса, поэтому мы приведём лишь примеры, которые иллюстрируют применение этой теоремы.
Пример 3Функция 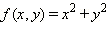 может быть преобразована следующим образом:
может быть преобразована следующим образом:
где
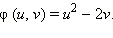
Пример 4Функция 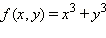 может быть преобразована следующим образом:
может быть преобразована следующим образом:
где
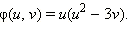
Аналогично, симметрическая функция трёх переменных определяется как функция, которая не изменяет своего значения при произвольных перестановках своих аргументов, то есть
Для симметрических многочленов трёх переменных справедлива точно такая же теорема, как и для многочленов двух переменных, а именно:
Теорема 2.
(о симметрических многочленах) Любой симметрический многочлен от трёх переменных представим в виде функции от трёх основных симметрических многочленов:
 |
Другими словами, для любого симметрического многочлена f (x, y) существует такая функция трёх переменных θ (u, v, w), что
Применим эту теорему для упрощения систем уравнений.
Пример 5Решите систему уравнений
Пример 6Решите систему уравнений
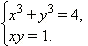 |
Эта система – симметрическая, поэтому делаем стандартную замену u = x + y, v = xy. Преобразуем левую часть первого уравнения: 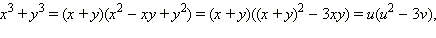 тогда система принимает вид:
тогда система принимает вид:
Итак, для u получаем уравнение 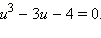 Вспомним теорему о рациональных корнях многочленов (§ 2.1.5). Рациональные корни нашего уравнения нужно искать среди делителей числа –4. Перебирая все делители, убеждаемся, что рациональных корней у уравнения нет. Однако эта теорема и не была теоремой существования корней. Указанная теорема констатировала лишь следующее: если у многочлена с целыми коэффициентами существуют рациональные корни (но для них имеется ещё возможность НЕ существовать), то эти корни будут иметь некоторый специальный вид. Тот случай, когда рациональных корней нет, эта теорема и не описывала.
Вспомним теорему о рациональных корнях многочленов (§ 2.1.5). Рациональные корни нашего уравнения нужно искать среди делителей числа –4. Перебирая все делители, убеждаемся, что рациональных корней у уравнения нет. Однако эта теорема и не была теоремой существования корней. Указанная теорема констатировала лишь следующее: если у многочлена с целыми коэффициентами существуют рациональные корни (но для них имеется ещё возможность НЕ существовать), то эти корни будут иметь некоторый специальный вид. Тот случай, когда рациональных корней нет, эта теорема и не описывала.
Попробуем найти корни уравнения исходной системы среди иррациональных чисел. Однако для этого придется проявить некоторую изобретательность: стандартная замена для симметрических систем здесь, очевидно не работает.
Возводя второе уравнение в куб, получим: 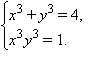 Таким образом, по теореме Виета,
Таким образом, по теореме Виета, 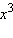 и
и 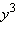 являются корнями квадратного уравнения
являются корнями квадратного уравнения 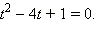 Отсюда
Отсюда 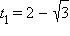 и
и 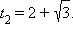 Значит,
Значит, 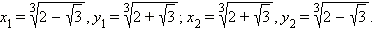
Заметим, что мы нашли один из корней уравнения 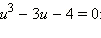
Ответ. 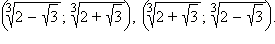
|
 |
 |
 |










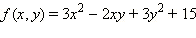 является симметрической функцией. В самом деле,
является симметрической функцией. В самом деле,
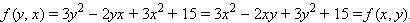
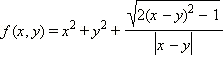 является симметрической. В самом деле,
является симметрической. В самом деле,
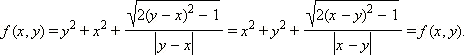
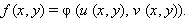
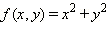 может быть преобразована следующим образом:
может быть преобразована следующим образом:
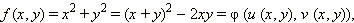
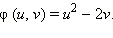
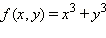 может быть преобразована следующим образом:
может быть преобразована следующим образом: