Глава 4. Комбинаторика
4.3.
4.3.4.
Случайной величиной называется числовая переменная величина, принимающая в зависимости от случая те или иные значения с определёнными вероятностями. Число попаданий в цель при данном числе выстрелов, скорость молекулы газа являются типичными примерами случайных величин.
Будем называть две случайные величины x и y взаимно независимыми, если события x = xi и y = yj являются взаимно независимыми.
Пример 1
 1 1
|
|
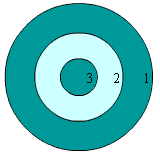
Найти закон распределения числа очков, которые выбивает стрелок на мишени, если вероятность его попадания в область 1 равна 0, вероятность попадания в область 2 равна 0,2, а в область 3 – 0,8.
Закон распределения можно представить в виде следующей таблицы:
|
Пример 2Пусть в мишень стреляют два стрелка. При этом закон распределения числа выбиваемых на мишени очков для первого стрелка задан таблицей:
Аналогичный закон распределения для второго стрелка задан таблицей:
Найдём закон распределения суммы очков, выбиваемых обоими стрелками.
Составим таблицу – закон распределения случайной величины x + y, где x – количество очков, выбиваемых первым стрелком, а y – количество очков, выбиваемых вторым стрелком.
| № |
x |
y |
x + y |
Вероятность результата |
| 1 |
1 |
1 |
2 |
0 ∙ 0,2 = 0 |
| 2 |
1 |
2 |
3 |
0 ∙ 0,5 = 0 |
| 3 |
1 |
3 |
4 |
0 ∙ 0,3 = 0 |
| 4 |
2 |
1 |
3 |
0,2 ∙ 0,2 = 0,04 |
| 5 |
2 |
2 |
4 |
0,2 ∙ 0,5 = 0,1 |
| 6 |
2 |
3 |
5 |
0,2 ∙ 0,3 = 0,06 |
| 7 |
3 |
1 |
4 |
0,8 ∙ 0,2 = 0,16 |
| 8 |
3 |
2 |
5 |
0,8 ∙ 0,5 = 0,4 |
| 9 |
3 |
3 |
6 |
0,8 ∙ 0,3 = 0,24 |
|
|
Значит, искомое распределение вероятностей задаётся таблицей
| 2 |
3 |
4 |
5 |
6 |
| 0 |
0,04 |
0,1 + 0,16 = 0,26 |
0,06 + 0,4 = 0,46 |
0,24 |















