Глава 4. Комбинаторика
4.3.
4.3.5.
Пусть мы измеряем случайную величину N раз, например, десять раз измеряем скорость ветра и хотим найти среднее значение. Как связано среднее значение с функцией распределения?
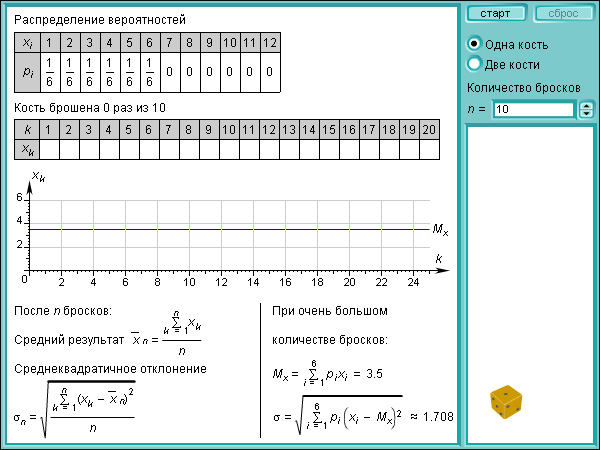
Будем кидать игральный кубик большое количество раз. Количество очков, которое выпадет на кубике при каждом броске, является случайной величиной и может принимать любые натуральные значения от 1 до 6. Среднее арифметическое выпавших очков, подсчитанных за все броски кубика, тоже является случайной величиной, однако при больших N оно стремится ко вполне конкретному числу – математическому ожиданию Mx. В данном случае Mx = 3,5.
Каким образом получилась эта величина? Пусть в N испытаниях 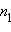 раз выпало 1 очко,
раз выпало 1 очко, 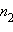 раз – 2 очка и так далее. Тогда
раз – 2 очка и так далее. Тогда 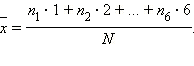 При N → ∞ количество исходов, в которых выпало одно очко,
При N → ∞ количество исходов, в которых выпало одно очко,
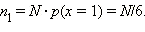 Аналогично,
Аналогично, 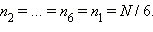 Отсюда
Отсюда
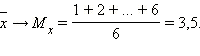

 |
|
Модель 4.5.
Игральные кости
|
Математическое ожидание случайной величины часто обозначается как <x>. Записи <x> и Mx эквивалентны.
Пример 1Найти математическое ожидание числа очков, которые выбьет первый стрелок в предыдущем примере.
Закон распределения рассматриваемой случайной величины может быть задан следующей таблицей:
Значит, 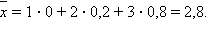
Ответ. 2,8.
|
Математическое ожидание не всегда является разумной оценкой какой-нибудь случайной величины. Так, для оценки средней заработной платы разумнее использовать понятие медианы, то есть такой величины, что количество людей, получающих меньшую, чем медиана, зарплату и большую, совпадают.
Другими словами, вероятность p1 того, что случайная величина x окажется меньшей x1/2, и вероятность p2 того, что случайная величина x окажется большей x1/2, одинаковы и равны 1/2. Медиана определяется однозначно не для всех распределений.
Вернёмся к случайной величине x, которая может принимать значения x1, x2, ..., xk с вероятностями p1, p2, ..., pk.
Используя вероятности pi того, что величина x принимает значения xi, эту формулу можно переписать следующим образом:
Пример 2В условиях предыдущего примера вычислить дисперсию и среднеквадратическое отклонение случайной величины x.
Имеем: Dx = 0 · (1 – 2,8)2 + 0,2 · (2 – 2,8)2 + 0,8 · (3 – 2,8)2 = 0,16.
Ответ. 0,16, 0,4.
|

 |
|
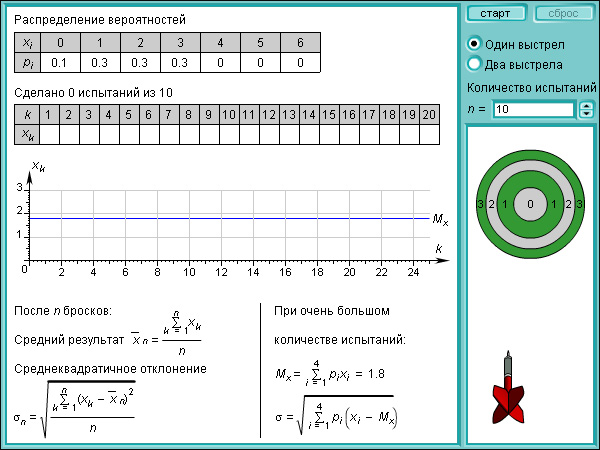
Модель 4.6.
Стрельба в мишень
|
Пример 3Найти распределение вероятности числа очков, выпавших на кубике с первого броска, медиану, математическое ожидание, дисперсию и среднеквадратичное отклонение.
Выпадение любой грани равновероятно, так что распределение будет выглядеть так:
| 1 |
2 |
3 |
4 |
5 |
6 |
| 1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
|
|
Математическое ожидание Mx = 3,5 (см. пример в начале параграфа).
С вероятностью 1/2 случайная величина x ≤ 3. С такой же вероятностью x ≥ 4. Таким образом, медианой случайной величины является любое число из интервала (3; 4). Обычно в качестве медианы указывают среднее значение из этого интервала: x1/2 = 3,5. В нашем случае медиана совпала с математическим ожиданием, в других распределениях это не так.
Дисперсия:
Среднеквадратичное отклонение 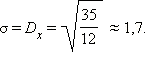 Видно, что отклонение величины от среднего значения очень велико.
Видно, что отклонение величины от среднего значения очень велико.
|
Свойства математического ожидания
- Математическое ожидание суммы независимых случайных величин равно сумме их математических ожиданий:
- Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
 |
Пример 4Найти математическое ожидание суммы и произведения очков, выпавшей на двух кубиках.
В примере 3 мы нашли, что для одного кубика M (x) = 3,5. Значит, для двух кубиков
| Mxy = Mx · My = 3,52 = 12,25. |
|
Свойства дисперсии
-
Дисперсия суммы независимых случайных величин равно сумме дисперсий:
 |
Пример 5Найти математическое ожидание и дисперсию суммы очков, выпавших при бросании кубика N раз.
Случайный процесс можно представить как сумму единичных бросков. Для единичного броска
Пусть за N бросков на кубике выпало y очков. Тогда
My = 3,5 N,
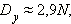
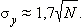 |
Если z – среднее количество очков, выпавших на кубике за N бросков: 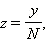 то:
то:
Этот результат верен не только для бросков кубика. Он во многих случаях определяет точность измерения математического ожидания опытным путем. Видно, что при увеличении количества измерений N разброс значений вокруг среднего, то есть среднеквадратичное отклонение, уменьшается пропорционально 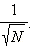
|
 Дисперсия случайной величины связана с математическим ожиданием квадрата этой случайной величины следующим соотношением:
 |
Действительно,
Найдём математические ожидания обеих частей этого равенства. По определению, 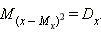 Математическое же ожидание правой части равенства по свойству математических ожиданий равно
Математическое же ожидание правой части равенства по свойству математических ожиданий равно 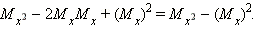 
|






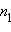 раз выпало 1 очко,
раз выпало 1 очко, 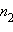 раз – 2 очка и так далее. Тогда
раз – 2 очка и так далее. Тогда 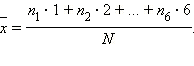 При
При 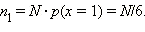 Аналогично,
Аналогично, 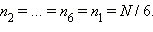 Отсюда
Отсюда