 Модель 4.5.
Модель 4.5.
 Модель 4.5.
Модель 4.5.
 |
Случайной величиной называется переменная величина, значения которой зависят от случая. Например, число попаданий в цель при данном числе выстрелов, скорость молекулы газа являются типичными примерами случайных величин. Случайной величиной является и результат бросания игральной кости, который и демонстрируется в этой интерактивной модели.
Для задания случайной величины нужно знать множество всевозможных её значений и вероятности, с которыми эта случайная величина принимает свои значения. Все эти данные образуют закон распределения случайной величины. В том случае, если кость одна, результат броска с равной вероятностью может быть равным 1, 2, 3, 4, 5 или 6. Вероятность каждого из исходов при этом равна 1/6. Если же игральных костей две, то вероятности различных исходов (под которыми в данном случае понимается сумма на костях) становятся не равными друг другу (так вероятность выпадения на двух костях 5 очков в сумме больше, чем вероятность выпадения двух очков).
Если случайная величина
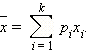 |
Дисперсией случайной величины называется среднее значение квадрата отклонения случайной величины от её среднего значения, то есть
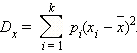 |
Среднеквадратическим отклонением случайной величины
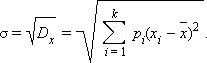 |
В интерактивной модели демонстрируются все перечисленные понятия на примере бросков игральной кости. Вы можете задать количество костей и количество бросков. После каждого броска подсчитывается среднее арифметическое всех исходов и строится график зависимости величины среднего арифметического от количества бросков. Это позволяет продемонстрировать опытным путем справедливость закона больших чисел.
Нажмите кнопку , чтобы начать анимацию, – чтобы приостановить её и – чтобы вернуть анимацию в исходное состояние.


