Глава 4. Комбинаторика
4.3.
4.3.6.
Пусть случайная величина принимает дискретные значения. К таким величинам, например, относятся количество очков при бросании кубика или количество угаданных номеров в лотерее «Спортлото». Вспомним, что закон распределения случайной величины образуют множество всевозможных её значений и вероятности, с которыми эта случайная величина принимает свои значения. Законы распределения могут быть вычислены исходя из логики процесса или измерены, если у нас есть достаточно большая статистическая выборка. Но для некоторых часто встречающихся типов процессов можно не выводить распределение, а использовать стандартное похожее. Рассмотрим наиболее известные из них.
1. Геометрическое распределение
Будем бросать кубик до тех пор, пока не выпадет 1. Посчитаем, с какой вероятностью это случится ровно за N бросков.
Для первого броска (N = 1), очевидно, вероятность успеха p (1) = 1/6.
Для второго (N = 2) это вероятность успеха во втором броске и неудачи в первом: 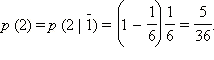
Аналогично, для третьего броска 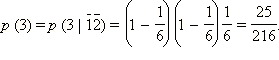
Вообще, для n-го броска 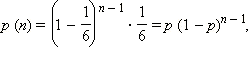 где p – вероятность успеха в единичном испытании.
где p – вероятность успеха в единичном испытании.
Математическое ожидание и дисперсия для этого распределения:
В нашем примере 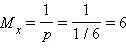 означает, что, в среднем, за шесть бросков 1 очко выпадет ровно 1 раз.
означает, что, в среднем, за шесть бросков 1 очко выпадет ровно 1 раз.
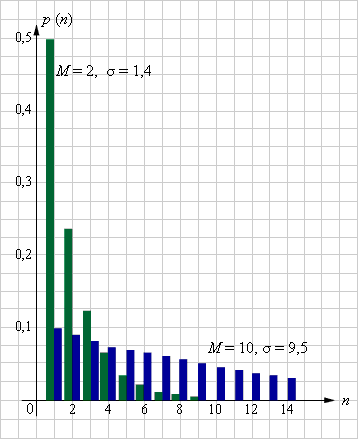 1 1
|
| Рисунок 4.3.6.1. Геометрическое распределение при различных p и n |
Пример 1Ролик кодового замка содержит N возможных цифр, из которых нужно выбрать одну. С какой вероятностью его можно открыть точно с k-го раза?
Вероятность правильного единичного выбора 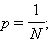 распределение, очевидно, геометрическое, поэтому
распределение, очевидно, геометрическое, поэтому
Если замок состоит из нескольких независимых роликов, то вероятность его случайного открывания подчиняется уже другому распределению – биномиальному.
|
2. Биномиальное распределение, часто возникающее в случайных процессах, можно получить так. Бросаем монету N раз и считаем вероятность того, что k раз из N выпала решка (будем обозначать это событие буквой P, а противоложное ему – выпадение герба – буквой О). Подумаем, какие распределения в этом случае можно считать равновероятными. Допустим, мы кинули монету три раза, при этом могли возникнуть такие комбинации:
ООО;
ООР; ОРО; РОО;
ОРР; РРО; РОР;
РРР.
Эти комбинации равновероятны.
Видно, что вероятность того, что событие «Р» наступит k раз из N, равна произведению:
- вероятности того, что k раз случилось событие «Р» – (p (Р))k. В нашем случае p = 1/2;
- вероятности того, что N – k раз случилось событие «не Р». В нашем случае это событие «О» – (p (О))N – k;
- числу перестановок
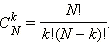
Таким образом, 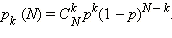
Распределение, описываемое формулой
называется биномиальным.
Математическое ожидание такого распределения легко посчитать из простых соображений. Поскольку результаты бросков кубика независимы, мы можем представить N бросков как N повторений одного броска. Напомним, что для N бросков
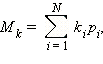 где
где 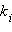 – число успехов, а
– число успехов, а 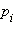 – вероятность того, что произойдет k успехов. Тогда математическое ожидание и дисперсия суммы испытаний равны сумме математических ожиданий и дисперсий одиночных событий:
– вероятность того, что произойдет k успехов. Тогда математическое ожидание и дисперсия суммы испытаний равны сумме математических ожиданий и дисперсий одиночных событий:
 2 2
|
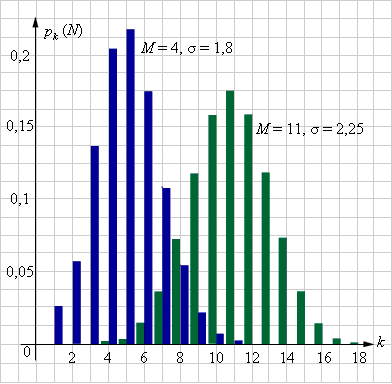
| Рисунок 4.3.6.2. Биномиальное распределение при различных параметрах
|
Пример 2Сосуд с N молекулами идеального газа мысленно разделён на две части, V1 и V2. Найти вероятность того, что в объёме V1 будет содержаться N1, а в объёме V2 будет содержаться N2 молекул.
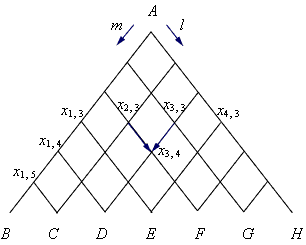
Пример 3Из пункта A по сети дорог идёт группа из N человек. На каждом перекрёстке, начиная с A, пришедшие туда люди с равной вероятностью поворачивают в направлении l и в направлении m. Сколько человек придёт в пункты B, C, D, …, I соответственно?
 3 3
|
| Рисунок 4.3.6.3
|
Допустим, что каждый человек уже повернул n раз. Все люди, вышедшие из пункта A, оказались в n-й строке. Обозначим число людей в каждой группе 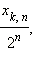 где k – номер группы, если их считать слева (см. рис. 4.3.6.3).
где k – номер группы, если их считать слева (см. рис. 4.3.6.3).
 4 4
|
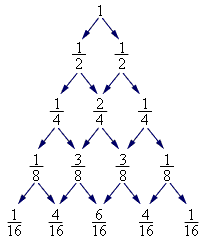
| Рисунок 4.3.6.4
|
Заметим, что в пункт (k, n) пришла примерно половина от числа людей из пунктов (k, n – 1) и (k – 1, n – 1), или:
Выписав 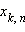
на соответствующих перекрёстках, мы получим треугольник Паскаля, коэффициенты которого равны 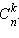
Значит, распределение вероятностей в k-й группе n-й строки – биномиальное c p = 0,5:
В нашем случае n = 6, и вероятность того, что человек окажется в k-м пункте, считая слева, равна
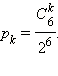
Если бы люди поворачивали вправо или влево с разной вероятностью, например, направо с вероятностью r, а налево – с вероятностью l = 1 – r, то распределение выглядело бы так:
|
Биномиальное распределение связано с задачами о случайных блужданиях и перемешиваниях.
Пример 4Пьяница случайным образом делает шаг вперёд или назад. Оцените, за какое количество шагов ему удастся добраться до дома, находящегося на расстоянии l от начала пути, при длине шага d?
Математическое ожидание положения человека в этой задаче равно нулю. Попасть домой человек сможет только случайно: если отклонится от начальной точки слишком далеко – как раз на расстояние до дома. Поэтому нам нужно найти не распределение вероятностей, а, фактически, среднеквадратичное отклонение длины пройденного пути за n шагов.
Перемещения за n и n + 1 шагов связаны соотношением
Возведём эту величину в квадрат и усредним:
Последний член просто равен математическому ожиданию, то есть нулю: 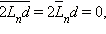 а а 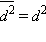 (величина d не является случайной). Тогда
(величина d не является случайной). Тогда
Это формула арифметической прогрессии, значит,
Отсюда средний пройденный за n шагов путь
Как уже было сказано выше, 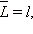 откуда
откуда 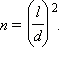
Видно, что для того, чтобы преодолеть расстояние в 10 шагов, несчастному придётся сделать 100 шагов. Если до дома 100 шагов, то придётся прошагать целых 10000 раз.
|
Задача о пьянице, в свою очередь, отсылает нас к важному классу задач о диффузии и случайному перемешиванию сыпучих тел. Для каждого реального процесса распределение вероятностей выводится отдельно, но биномиальное распределение используется очень часто. Что будет, если увеличить количество испытаний N и шагать в одну сторону с очень маленькой вероятностью p, а в другую – с вероятностью, близкой к единице? Например, предположим, что Np → λ. При этих предположениях биномиальное распределение переходит в распределение Пуассона.
3. Распределение Пуассона имеет следующую плотность вероятности:
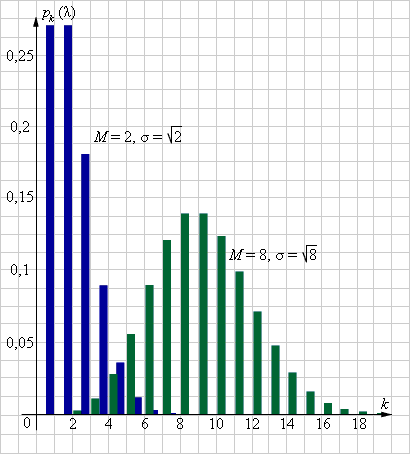
Величина pk (λ) соответствует вероятности ровно k удачных исходов при условии, что среднее число удачных исходов составляет λ.
Этим распределением проще пользоваться, чем биномиальным. Параметр λ (напомним, что он определяется пределом Np → λ) здесь равен числу, которое соответствует математическому ожиданию величины x:
 5 5
|
| Рисунок 4.3.6.5. Распределение Пуассона при различных λ и n |
Пример 5В супе объёмом V плавает N перчинок. С какой вероятностью в ложку объёмом V0 попадёт ровно n перчинок?
Если количество перчинок N велико, а отношение 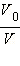 мало, то задача описывается распределением Пуассона.
мало, то задача описывается распределением Пуассона.
В среднем, в ложке должны оказаться 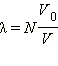 перчинок. Вероятность того, что в ложке окажется ровно n перчинок, равна
перчинок. Вероятность того, что в ложке окажется ровно n перчинок, равна  В частности, при V = 10 л,
В частности, при V = 10 л, 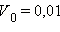 л, N = 50 получаем
л, N = 50 получаем 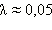 (то есть одна перчинка, в среднем, попадается на 20 ложек), а вероятность:
(то есть одна перчинка, в среднем, попадается на 20 ложек), а вероятность:
- того, что в ложке окажется ноль перчинок, p0 ≈ 0,95123,
- того, что в ложке окажется одна перчинка, p1 ≈ 0,04756,
- того, что в ложке окажется две перчинки, p2 ≈ 0,00119,
- того, что в ложке окажется три перчинки, p3 ≈ 0,00002.
Как видим, pn очень быстро уменьшается с ростом n.
|
Распределением Пуассона описываются процессы типа количества телефонных вызовов за время t, вероятности аварий, оно же используется в теории страхования.






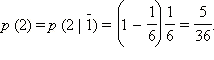
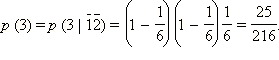
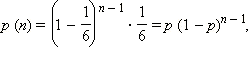 где
где 



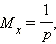
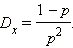
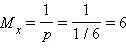 означает, что, в среднем, за шесть бросков 1 очко выпадет ровно 1 раз.
означает, что, в среднем, за шесть бросков 1 очко выпадет ровно 1 раз. 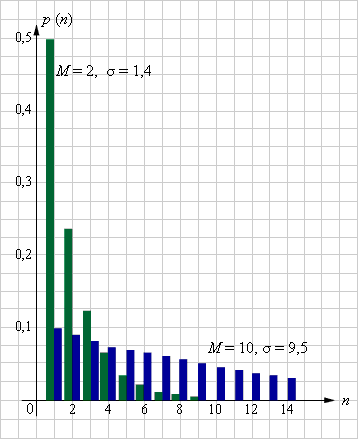
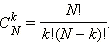
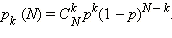
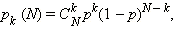




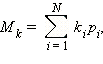 где
где 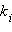 – число успехов, а
– число успехов, а 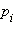 – вероятность того, что произойдет
– вероятность того, что произойдет