

 |
 |
 |
 |
|
 |
 |
|
Вернемся к стрелку, на примере которого мы вводили понятие дискретного распределения вероятностей. Тогда мы рассматривали результат его стрельбы в виде номера круга, в который он попал. Теперь же представим, что, попадая в мишень, стрела оставляет на мишени точку. Вероятность того, что стрела два раза попадёт в одно и то же место, очень мала, поэтому можно считать, что точки не пересекаются. Мы увидим примерно такую картинку.
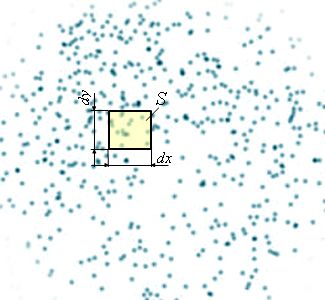 |
| Рисунок 4.3.7.1 |
Если разделить количество точек, попавших в небольшой квадрат площадью
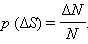 |
Здесь мы предполагаем, что площадка
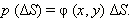 |
При устремлении площади квадратика к нулю (вспомните школьный курс интегрального исчисления) конечные разности нужно заменить на дифференциалы: 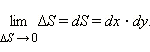 Итак,
Итак,
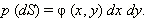 |
Если нам нужно будет узнать вероятность, с которой стрелок попадает в площадку мишени, на которой плотность вероятности нельзя считать постоянной, эту функцию придется интегрировать.
Плотность вероятности существует и для распределений, зависящих от одной переменной. Рассмотрим это на следующем примере.
Пусть
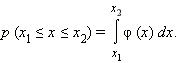 |
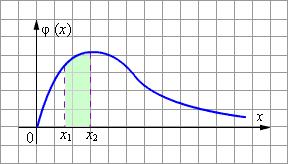 |
| Рисунок 4.3.7.2 |
Отсюда следует важное свойство плотности вероятности. Поскольку попадание случайной величины
Нормировка плотности распределения вероятности
|
Для некоторого случайного процесса график зависимости плотности вероятности от значения переменной
 |
| Рисунок 4.3.7.3 |
Найти величину
Математическое ожидание величины
|
Среднеквадратичное отклонение по-прежнему задается формулой
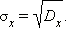 |
Вообще, в том случае, если плотность распределения случайной величины
|
Так же, как и для дискретных процессов, для непрерывной случайной величины существуют несколько характерных распределений вероятностей.
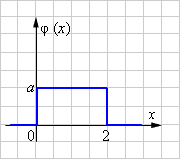
Распределение, частный случай которого приведён в примере 1, называется постоянным распределением. Его плотность принимает одно и то же значение 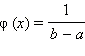 на некотором отрезке
на некотором отрезке 
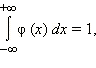 становится ясно, что значение
становится ясно, что значение
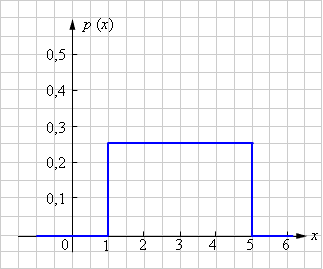 |
| Рисунок 4.3.7.4. Плотность вероятности постоянного распределения при |
Вычислить математическое ожидание, дисперсию, среднеквадратичное отклонение случайной величины 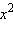 для постоянного распределения
для постоянного распределения 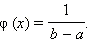
2. Экспоненциальное, или показательное распределение
Рассмотрим прохождение потока частиц через какое-либо вещество. Часть частиц будет поглощаться веществом. Разделим мысленно среду на тонкие пластинки, и пусть, проходя через каждую пластинку, количество частиц в потоке уменьшается в
В реальных условиях процесс поглощения частиц всегда случаен. Можно сказать, что вероятность обнаружить частицу после прохождения через  где
где 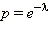 и
и 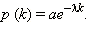 Устремим ширину пластинки к нулю, одновременно увеличивая количество пластинок. В этом случае можно записать, что вероятность обнаружить частицу на глубине
Устремим ширину пластинки к нулю, одновременно увеличивая количество пластинок. В этом случае можно записать, что вероятность обнаружить частицу на глубине 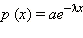
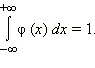 Так как выражение
Так как выражение 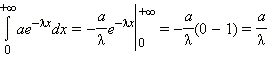 равно единице по условию нормировки, то
равно единице по условию нормировки, то
Плотность вероятности экспоненциального распределения описывается формулой
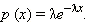 |
Его математическое ожидание и среднеквадратичное отклонение можно получить путём интегрирования по частям. Пропуская вычисления, запишем сразу результат:
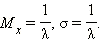 |
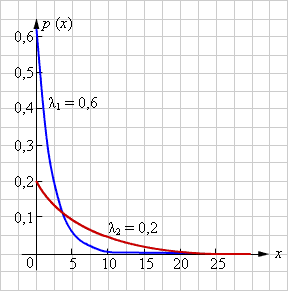 |
| Рисунок 4.3.7.5. Плотность вероятности экспоненциального распределения
|
Вероятность того, что лампочка перегорит ровно через
3. Рассматривая в предыдущем параграфе дискретные распределения, мы говорили о том, что если распределение вероятностей вызвано сложением большого количества случайных событий, каждое из которых мало влияет на результат, то это, скорее всего, распределение Пуассона. В аналогичном непрерывном случае получается распределение Гаусса, которое часто называют нормальным распределением.
Плотность вероятности нормального распределения имеет вид:
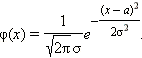 |
В этой формуле
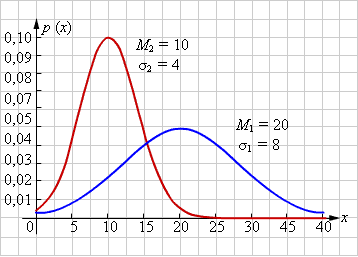 |
| Рисунок 4.3.7.6. Плотность вероятности нормального распределения
|
Сумма двух нормальных распределений с параметрами 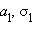 и
и 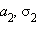 также является нормальным распределением с параметрами
также является нормальным распределением с параметрами 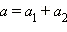 и
и 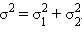
Показания счётчика Гейгера, регистрирующего количество пролетевших сквозь него за 1 секунду элементарных частиц, подчиняются распределению 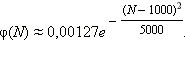 Найдите математическое ожидание показаний счётчика.
Найдите математическое ожидание показаний счётчика.
Определите среднее значение скорости молекул газа, если закон распределения скоростей молекул задаётся формулой Максвелла
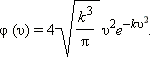 |
Нормальному распределению подчиняются случайные ошибки измерений.
4. Частным случаем нормального распределения является логарифмически нормальное. Оно легко получается из нормального заменой
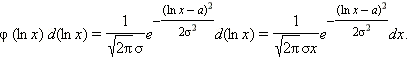 |
Здесь учтено, что 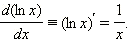
Плотность логарифмически нормального распределения
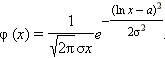 |
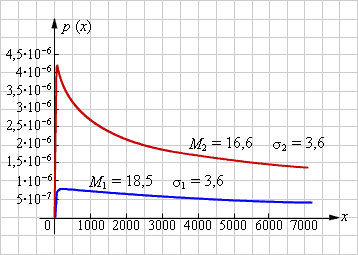 |
| Рисунок 4.3.7.7. Плотность вероятности логнормального распределения
|

 |
|
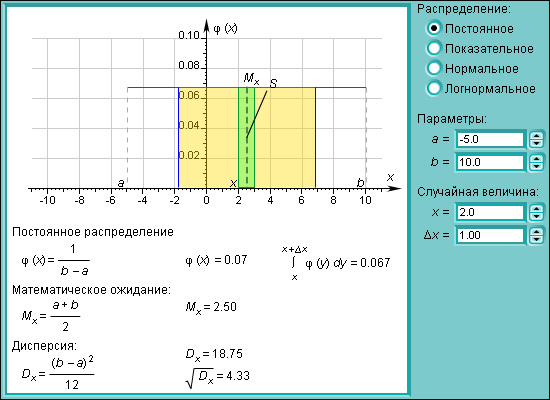
Модель 4.7.
Распределения вероятностей
|
 |
 |
 |

