|
|
Полученные при непосредственном измерении величины неизбежно содержат ошибки, обусловленные самыми разными причинами. Среди этих ошибок следует различать систематические и случайные.
Систематические ошибки обусловливаются причинами, действующими вполне определённым образом. Примером систематической ошибки при взвешивании может являться смещение стрелки ненагруженных весов относительно нулевой отметки на некоторую постоянную величину
Случайные ошибки вызываются большим числом отдельных причин, действующих в каждом отдельном измерении различными способами. В примере со взвешиванием это могут быть незаметные глазу колебания чаши весов, потоки воздуха, толчки фундамента здания, в котором стоят весы. Эти ошибки полностью исключить невозможно.
 Полная ошибка измерения принимается равной сумме случайной и систематической ошибок:
|
Определите, какие ошибки из перечисленных являются случайными:
1) ошибка при однократном измерении сопротивления проводника;
2) отклонение значения сопротивления проводника от измеренного более точным прибором в процессе измерения сопротивления одного и того же проводника 100 раз в одну и ту же сторону;
3) однократное измерение диаметра сосуда;
4) отклонение значения внутреннего диаметра одного и того же сосуда при измерении 30 раз в разные стороны.
Случайная ошибка, возникающая при измерении некоторой величины, может теоретически принимать любые значения. Она является непрерывной случайной величиной, подчинённой определённому закону распределения вероятности.
Наиболее часто встречающиеся на практике ошибки распределены по нормальному закону:
 |
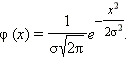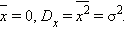
С какой вероятностью измеренная величина будет отклоняться от своего точного значения не больше, чем на σ? Очевидно с той же самой, с которой ошибка измерения будет находиться в промежутке [–σ; σ]. Если случайная ошибка распределена по нормальному закону, то для ответа на этот вопрос необходимо вычислить интеграл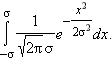 
Расчёты показывают, что в 68,27 % отклонения случайной величины, распределённой по нормальному закону, не превышают σ, в 95,45 % – 2σ. Наконец, вероятность того, что случайная величина, распределённая нормально, отклоняется от математического ожидания больше, чем на 3σ, пренебрежимо мала и составляет 0,27 % – правило трёх сигм.
 |
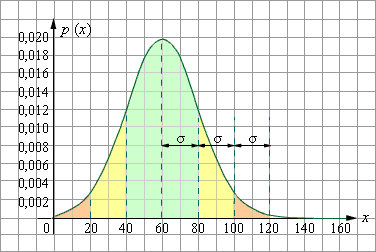| Рисунок 4.3.8.1. Правило трёх сигм
|
|
|
 |
