|
|
Пусть
 |
 |
 |
|
||
 |
|
 |
В школе 1254 учащихся. При округлении этого числа до 1200 абсолютная погрешность составляет Δ = |1200 – 1254| = 54, а при округлении до 1250: Δ = |1250 – 1254| = 4.
Определите абсолютную погрешность измерения длины точной миллиметровой линейкой.
Вообще, если систематические ошибки, возникающие при измерении каким-либо прибором, значительно меньше, чем деления шкалы этого прибора, то в качестве абсолютной погрешности измерения обычно берут половину деления.
|
|
|
|
||
|
|
|
В школе 1254 учащихся. При округлении этого числа до 1200 абсолютная погрешность составляет Δ = |1200 – 1254| = 54, относительная погрешность равна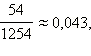 
или 4,3 %. При округлении до 1250: Δ = |1250 – 1254| = 4, а относительная погрешность 
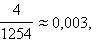или 0,3 %.
В научных экспериментах многие величины определяются не непосредственно, а косвенным путём – измерением значений других величин. Так, чтобы найти плотность тела, ученые измеряют его массу, взвешивая на весах, после чего определяют объём тела, погружая его в жидкость. Плотность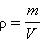 
выражается через массу и объём тела. Масса и объём, входящие в эту формулу, измеряются с некоторой погрешностью; это означает, что и плотность будет вычислена по формуле с некоторой погрешностью.
Выведем несколько правил, позволяющих рассчитывать погрешности величин.
Абсолютная погрешность суммы двух независимых величин равна сумме абсолютных погрешностей отдельных слагаемых:
|
Отметим, что в отдельных измерениях может случиться, что ошибки в измерении величин
Аналогично можно показать, что то же самое верно для разности двух погрешностей.
Абсолютная погрешность разности двух независимых величин равна сумме абсолютных погрешностей уменьшаемого и вычитаемого:
|
Относительные погрешности при сложении и вычитании складывать нельзя. Рассмотрим поучительный пример.
Измерения цилиндрической полой изнутри трубы показали, что ее внешний радиус равен 100 см, а внутренний радиус – 95 см. Чему равна толщина стенок трубы?
 |
|
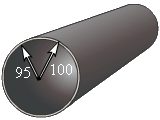Если Рассчитаем теперь относительные погрешности всех трёх величин: |
Относительная погрешность произведения приближённо равна сумме относительных погрешностей отдельных сомножителей:
|
Можно расширить это правило, расписав его для произведения
Относительная погрешность
|
Расчёты показывают, что это соотношение верно не только для натуральных, но и для любых вещественных степеней
В частности,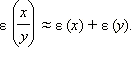 
Вычислите относительную погрешность произведения 0,123 и 0,526, если относительные погрешности этих чисел соответственно равны 2 % и 4 %.
|
|
 |
Если оба радиуса были измерены с погрешностью порядка 0,5 %, то погрешность при вычислении их разности – толщины стенок трубы – возросла в 100 раз и составила 50 %!
и 
Тогда
