 Модель 4.7.
Модель 4.7.
 Модель 4.7.
Модель 4.7.
 |
Если случайная переменная величина
Математическое ожидание (среднее значение) для непрерывного распределения описывается формулой 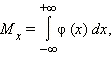 а дисперсия (квадрат среднеквадратичного отклонения) – формулой
а дисперсия (квадрат среднеквадратичного отклонения) – формулой 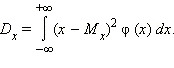 Среднеквадратичное отклонение часто обозначается буквой σ.
Среднеквадратичное отклонение часто обозначается буквой σ.
Простейшим непрерывным распределением является распределение с постоянной плотностью 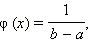 где
где 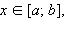
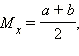 а дисперсия
а дисперсия 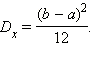
Наиболее изученным и имеющим широкое применение является так называемый нормальный закон распределения:
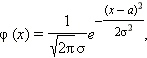 |
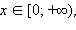
В частности, нормальный закон используется в анализе случайных ошибок наблюдения (распределение Гаусса), в молекулярно-кинетической теории (распределение Максвелла). Математическое ожидание для этого распределения 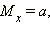 а среднеквадратичное отклонение равно σ. График плотности нормального распределения симметричен относительно вертикальной прямой
а среднеквадратичное отклонение равно σ. График плотности нормального распределения симметричен относительно вертикальной прямой  Чем меньшую дисперсию
Чем меньшую дисперсию 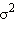 имеет распределение, тем более узким и высоким становится максимум.
имеет распределение, тем более узким и высоким становится максимум.
Логарифмически-нормальное (логнормальное) распределение имеет плотность вероятности
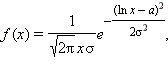 математическое ожидание
математическое ожидание 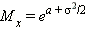 и дисперсию
и дисперсию 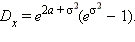 Этому распределению подчиняется, например, размер частиц при дроблении какого-либо материала.
Этому распределению подчиняется, например, размер частиц при дроблении какого-либо материала.
Показательное распределение описывается формулами 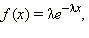
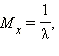
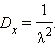
В нормальном распределении случайная величина
Существуют также и другие непрерывные функции распределения вероятности.
В интерактивном режиме вы можете выбрать тип распределения, его основные параметры, ввести значения


