Глава M. Методика

M.3.

M.3.6.

Тема. Алгебраические уравнения.

Основные понятия. Определение алгебраического уравнения, алгоритм решения алгебраического уравнения.

Самостоятельная деятельность учащихся. Решение задач по теме «Алгебраические уравнения».

Использование новых информационных технологий. В качестве дополнительного иллюстративного материала показ на компьютере модели курса «Алгебраические уравнения» (используется компьютерная модель 2.3. Сложение и вычитание алгебраических дробей).

План урока

Основное содержание урока

Решение рациональных уравнений базируется на умении и отработке навыков работы с алгебраическими дробями. Мы считаем целесообразным поработать с моделью 2.3.

В модели 2.3 вы найдёте:

1. алгоритм приведения дробей к общему знаменателю;
2. правило сложения и вычитания алгебраических дробей;
3. применение алгоритма сложения и вычитания алгебраических дробей на конкретных примерах.

Мы рекомендуем рассмотреть решение примеров, данных в модели 2.3, и разобрать их с учащимися.

Выполните действие:

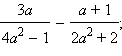
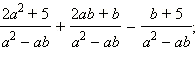
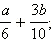
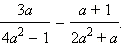
	Если r (x) – рациональное выражение, то уравнение r (x) = 0 называют рациональным уравнением.

Алгоритм решения рационального уравнения

1. Перенести все члены уравнения в одну часть.
2. Преобразовать эту часть уравнения к виду алгебраической дроби
3. Решить уравнение p (x) = 0.
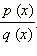
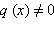4. Для каждого корня уравнения p (x) = 0 сделать проверку: удовлетворяет ли он условию или нет. Если да, то это – корень заданного уравнения; если нет, то это – посторонний корень, и в ответ его включать не следует.

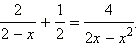
Решение.

Будем действовать в соответствии с алгоритмом.

1. Преобразуем уравнение к виду
2. Выполним преобразование левой части этого уравнения (приведение алгебраической дроби к общему знаменателю известно учащимся). После тождественных преобразований данное уравнение принимает вид
3. Решим уравнение x² – 6x + 8 = 0. Находим: x₁ = 4; x₂ = 2.

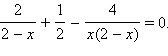
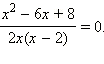
4. Для найденных значений проверим выполнения условия 2x(x – 2) ≠ 0.

   Число 4 этому условию удовлетворяет, а число 2 – нет. Значит, 4 – корень заданного уравнения, а 2 – посторонний корень.

Ответ: 4.

Далее приведём подборку примеров для отработки алгоритма решения рационального уравнения.

Решите уравнение

1. 
2. 
3. 
4. 
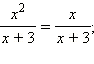
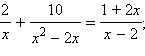
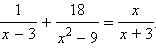
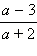5. При каких значениях a значения дробей и 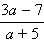равны?
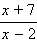6. Существуют ли такие значения переменной, при которых сумма дробей и 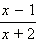равна 1?
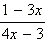7. При каких значениях переменной разность дробей и 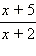равна их произведению?
   

   Решите уравнение, используя метод введения новой переменной:

8. x⁴ – 17x² + 16 = 0;
9. 9x⁴ – 40x² + 16 = 0;
10. 10x⁶ – 7x³ – 8 = 0;
11. (3x – 4)² – 5(3x – 4) + 6 = 0;
12. 2(7x – 6)² + 3(7x – 6) + 1 = 0;
13. (x² + 2x)² – 2(x² + 2x) – 3 = 0;
14. 2(x² + 2x + 1)² – (x + 1)²  = 1;
15. * (x² – 3x + 1)(x² – 3x + 3) = 3;
16. *
17. * (x² – 5x + 7)² – (x – 2)(x – 3) = 1;
18. *
19. * x(x – 1)(x – 2)(x – 3) = 15;
20. * (x + 1)(x + 2)(x + 3)(x + 4) = 3;
21. *
22. *

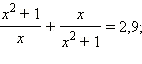
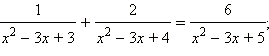
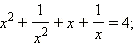
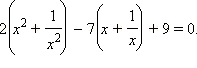
Ответы на вопросы

1. Какое уравнение называется рациональным?
2. Сформулируйте алгоритм решения рационального уравнения.

Домашнее задание

1. № 1031–1061 из задачника А. Г. Мордковича, Т. Н. Мишустиной, Е. Е. Тульчинской, алгебра, 8 класс.