Глава M. Методика

M.3.

M.3.5.

Тема. Свойства логарифмов.

Основные понятия. Логарифм произведения, логарифм частного, логарифм степени.

Самостоятельная деятельность учащихся. Решение задач по теме «Свойства логарифмов».

Использование новых информационных технологий. В качестве дополнительного иллюстративного материала показ на компьютере модели курса «Свойства логарифмов» (используется компьютерная модель 3.1. Решение логарифмических уравнений).

План урока

Основное содержание урока

Чтобы успешно использовать на практике операцию логарифмирования, нужно познакомиться со свойствами этой операции.

Все свойства формулируются и доказываются только для положительных значений переменных, содержащихся под знаками логарифмов.

Теорема 1.  Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел: loga bc = loga b + loga c.

Приведём краткую запись доказательства теоремы. Подготовка к доказательству (введение новых переменных) Перевод на более простой язык Доказательство loga bc = x loga b = y loga c = z Доказать: x = y + z ax = bc ay = b az = c ax = ayaz ax = ay + z x = y + z

Теорема 2.  Если a, b, c – положительные числа, причём a ≠ 1, то справедливо равенство

Краткая формулировка, которую удобно использовать на практике: логарифм частного равен разности логарифмов делимого и делителя, или логарифм дроби равен разности логарифмов числителя и знаменателя.

Приведём краткую запись доказательства теоремы. Подготовка к доказательству (введение новых переменных) Перевод на более простой язык Доказательство loga b = y loga c = z Доказать: x = y – z ay = b az = c ax = ay : az ax = ay - z x = y - z

Теорема 3.  Если a и b – положительные числа, причём a ≠ 1, то для любого числа r справедливо равенство loga br = r loga b.

Краткая формулировка, которую удобно использовать на практике: логарифм степени равен произведению показателя степени на логарифм основания степени.

Приведём краткую запись доказательства теоремы. Подготовка к доказательству (введение новых переменных) Перевод на более простой язык Доказательство loga br = x loga b = y Доказать: x = y · r ax = br ay = b ax = (ay)r ax = ayr x = y · r

Приведём систему упражнений, с помощью которой можно отработать свойства логарифмов на практике. Эти задания напрямую связаны с применением теорем 1, 2, 3.

    Вычислите

1. log₆ 2 + log₆ 3;
2. lg 25 + lg 4;
3. log₁₄₄ 3 + log₁₄₄ 4;
4. 
5. 
6. 
7. 
8. (3 lg 2 – lg 24) : (lg 3 + lg 27);
9. (log₃ 2 + 3log₃ 0,25) : (log₃ 28 – log₃ 7);
10. 
    
11. Известно, что log₅ 2 = a. Найдите log₅ 10.
12. Известно, что log₆ 42 = b. Найдите log₆ 7.
13. Решите уравнение log₄ x = log₄ 2 + log₄ 7.
14. Решите уравнение log₂ 3x = log₂ 4 + log₂ 6.
15. Решите уравнение log_x 8 – log_x 2 = 2.

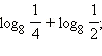
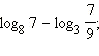
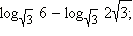
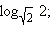
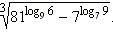
После разбора данных примеров полезно поработать с моделью 3.1, в которой показано применение свойств логарифмов при решении логарифмических уравнений. В этой модели показано два метода решения логарифмических уравнений:

1. метод потенцирования на примере решения уравнения;
2. метод введения новой переменной на примере решения уравнения.

После разбора данных примеров можно сделать «мостик» на следующие уроки, то есть обсудить с учащимися, какие методы мы подробно будем изучать, какие уравнения будем решать и каким методом, используя свойства логарифмов.

1. Какие свойства логарифмов вы знаете?
2. Чему равен логарифм произведения?
3. Чему равен логарифм частного?
4. Чему равен логарифм степени?

Домашнее задание.

№ 1495–1546 из задачника: А. Г. Мордкович и др. Алгебра и начала анализа, 10–11 класс.