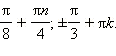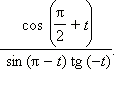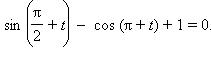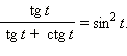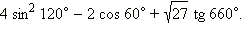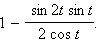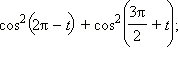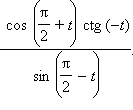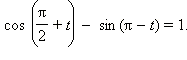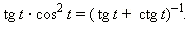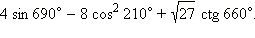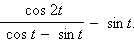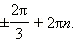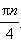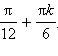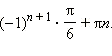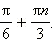Глава M. Методика
M.3.
M.3.9.
Тип урока: итоговый контроль (проводится двухчасовая контрольная работа)Тема. Соотношение между тригонометрическими функциями одного и того же аргумента.
Основные понятия. Преобразование тригонометрических выражений с использованием формул приведения, основного тригонометрического тождества, теорем сложения, формул двойного аргумента, формул понижения степени, а также формул, связанных с преобразованием суммы в произведение.
Самостоятельная деятельность учащихся. Решение контрольной работы по теме «Соотношения между тригонометрическими функциями одного и того же аргумента».
Использование новых информационных технологий. В качестве дополнительного иллюстративного материала показ на компьютере модели курса «Делители и кратные» перед проведением контрольной работы (используются компьютерные модели 2.7, 2.8, 2.9, 2.10).
План урока
| Этапы урока |
Время, мин |
Приёмы и методы |
| I. Проведение контрольной работы по теме «Соотношения между тригонометрическими функциями одного и того же аргумента» |
90 |
Контрольная работа |
Перед проведением контрольной работы полезно вспомнить с учащимися свойства и графики тригонометрических функций. В этой ситуации мы рекомендуем поработать с моделями 2.7, 2.8, 2.9, 2.10.
Модель 2.7. Функция y = sin x.В этой модели строятся графики функций вида y = A sin (ax + b) + B. Мы рекомендуем ввести следующие значения параметров:
A = 1, B = 0, a = 1, b = 0.
В итоге получим график функции y = sin x.
Используя данную модель, можно предложить учащимся ответить на следующие вопросы:
- Какова область определения функции?
- Какова область её значений?
- Является ли функция непрерывной?
- На каких промежутках функция возрастает, на каких убывает?
- Является ли функция чётной или нечётной?
- Как выглядят графики чётной, нечётной функций?
- Вычислите f (0); f (π); f (π/2); f (–π/2); f (–π); f (2π); f (–2π); f (3π/2).
Модель 2.8. Функция y = cos x.В этой модели строятся графики функций вида y = A cos (ax + b) + B. Мы рекомендуем ввести следующие значения параметров:
A = 1, B = 0, a = 1, b = 0.
В итоге получим график функции y = cos x.
Используя данную модель, можно предложить учащимся ответить на следующие вопросы:
- Какова область определения функции?
- Какова область её значений?
- Является ли функция непрерывной?
- На каких промежутках функция возрастает, на каких убывает?
- Является ли функция чётной или нечётной?
- Как выглядят графики чётной, нечётной функций?
- Вычислите f (0); f (π); f (π/2); f (–π/2); f (–π); f (2π); f (–2π); f (3π/2).
Модель 2.9. Функция y = tg x.В этой модели строятся графики функций вида y = A tg (ax + b) + B. Мы рекомендуем ввести следующие значения параметров:
A = 1, B = 0, a = 1, b = 0.
В итоге получим график функции y = tg x.
Используя данную модель, можно предложить учащимся ответить на следующие вопросы:
- Какова область определения функции?
- Какова область её значений?
- Является ли функция непрерывной?
- На каких промежутках функция возрастает, на каких убывает?
- Является ли функция чётной или нечётной?
- Как выглядят графики чётной, нечётной функций?
- Вычислите f (0); f (π); f (π/2); f (–π/2); f (–π); f (2π); f (–2π); f (3π/2).
Модель 2.10. Функция y = ctg x.В этой модели строятся графики функций вида y = A ctg (ax + b) + B. Мы рекомендуем ввести следующие значения параметров:
A = 1, B = 0, a = 1, b = 0.
В итоге получим график функции y = ctg x.
Используя данную модель, можно предложить учащимся ответить на следующие вопросы:
- Какова область определения функции?
- Какова область её значений?
- Является ли функция непрерывной?
- На каких промежутках функция возрастает, на каких убывает?
- Является ли функция чётной или нечётной?
- Как выглядят графики чётной, нечётной функций?
- Вычислите f (0); f (π); f (π/2); f (–π/2); f (–π); f (2π); f (–2π); f (3π/2).
Основное содержание урока
Вариант 1
-
Упростите выражение:
а) sin2 (π + t) – sin2 (π – t);
б) 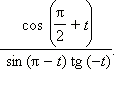
-
Решите уравнение
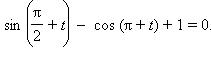
-
Упростите выражение:
cos (–t) + sin (π + t).
-
Докажите тождество:
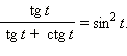
-
Вычислите
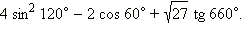
-
Докажите тождество:
sin (α + β) + sin (α – β) = 2 sin α cos β.
-
Решите уравнение
sin 3x cos x + cos 3x sin x = 0.
-
Упростите выражение:
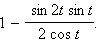
-
Решите уравнение
sin 7x = sin 5x.
-
Докажите тождество:
2cos2 (45° + 3α) + sin 6α = 1.
-
Вычислите
cos 50° + sin 160° – cos 10°.
-
Решите уравнение
sin 6x + sin 2x + 2sin2 x = 1.
Вариант 2
-
Упростите выражение:
а) 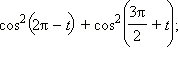
б) 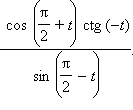
-
Решите уравнение
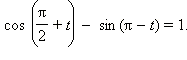
-
Упростите выражение:
ctg (–t) sin t + cos (π + t).
-
Докажите тождество:
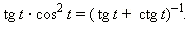
-
Вычислите
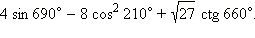
-
Докажите тождество:
cos (α + β) + cos (α – β) = 2 cos α cos β.
-
Решите уравнение
cos 2x cos x – sin 2x sin x = 0.
-
Упростите выражение:
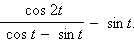
-
Решите уравнение
cos 6x = cos 4x.
-
Докажите тождество:
2 sin2 (45° – 3α) + sin 6α = 1.
-
Вычислите
sin 84° + cos 234° – sin 24°.
-
Решите уравнение
2 cos2 2x + cos 2x + cos 6x = 1.
Ответы
Вариант 1
- а) 0; б) ctg t.
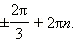
- 0.
- Тождество верно.
- 1.
- Тождество верно.
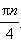
- cos 2t.
- πn;
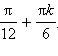
- Тождество верно.
- 0.
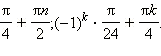
Вариант 2
- а) 1; б) 1.
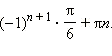
- –2 cos t.
- Тождество верно.
- –11;
- Тождество верно.
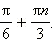
- cos t.
- πn;
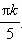
- Тождество верно.
- 0.