Глава 1. Теоретические сведения о функциях

1.2. Системы координат

1.2.2. Полярная и сферическая системы координат

Для определения координат в декартовой системе координат используются координатные оси. Однако в ряде случаев удобно в качестве координат использовать не метрические величины, а величины других размерностей, например, углы.

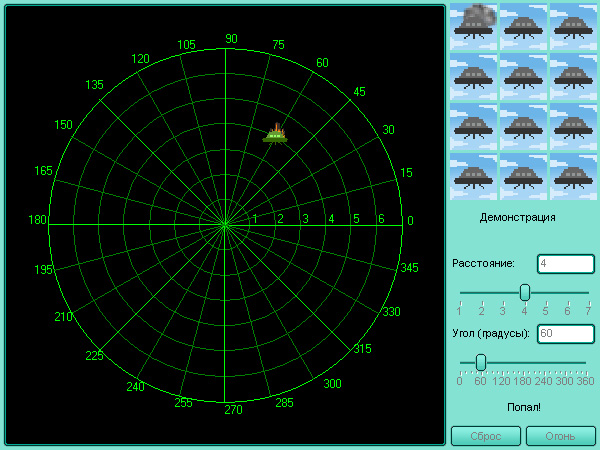
Модель 1.6. Воздушная атака

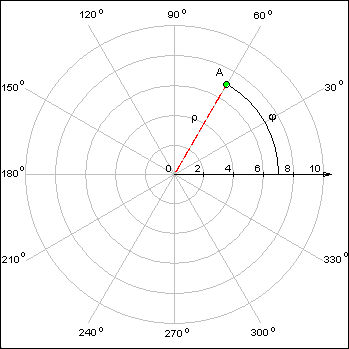
Полярная система координат ставит в соответствие каждой точке на плоскости пару чисел (ρ; φ). Основными понятиями этой системы являются точка отсчета – полюс – и луч, начинающийся в этой точке, – полярная ось. Координата ρ – расстояние от точки до полюса, координата φ – угол между полярной осью и отрезком, соединяющим полюс и рассматриваемую точку, который берется со знаком «+», если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «–» в противоположном случае. Важно понимать, что число φ в полярной системе определено не однозначно: парам чисел (ρ; φ + 2πn) соответствует одна и та же точка при любых натуральных n. Для полюса ρ = 0, а угол φ не определен.

1

Рисунок 1.2.2.1. Полярная система координат

Полярные координаты легко преобразовать в декартовы. Пусть (x; y) – координаты точки в декартовой системе координат, (ρ; φ) – в полярной. Тогда очевидно, что

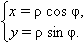Формулы обратного перехода:

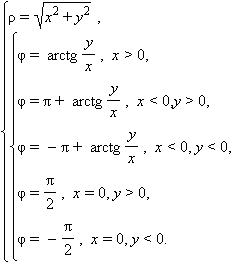Полярную систему можно обобщить на трехмерный случай: для этого придется ввести третью координату – угол θ. Углы φ и θ примерно соответствуют земным долготе и широте (угол θ также отсчитывается от «экватора»), а координата ρ определяет расстояние от исследуемой точки до полюса. Подобная система координат носит название сферической. Сферическими координатами точки в трехмерном пространстве являются:

• ρ – расстояние от точки до полюса,
• φ – угол между полярной осью и проекцией радиус-вектора точки на выбранную экваториальную плоскость (содержащую полярную ось),
• θ – угол между радиус-вектором точки и его проекцией на экваториальную плоскость.

Система координат, состоящая из полюса, экваториальной плоскости и полярной оси, лежащей в ней, называется сферической.

2

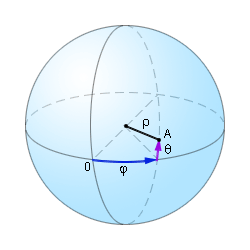
Рисунок 1.2.2.2. Сферическая система координат