

 |
 |
Основным отличием жидкостей от твердых (упругих) тел является способность легко изменять свою форму. Части жидкости могут свободно сдвигаться, скользя друг относительно друга. Поэтому жидкость принимает форму сосуда, в который она налита. В жидкость, как и в газообразную среду, можно погружать твердые тела. В отличие от газов жидкости практически несжимаемы.
На тело, погруженное в жидкость или газ, действуют силы, распределенные по поверхности тела. Для описания таких распределенных сил вводится новая физическая величина – давление.
Давление определяется как отношение модуля силы 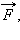 действующей перпендикулярно поверхности, к площади
действующей перпендикулярно поверхности, к площади
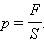 |
В системе СИ давление измеряется в паскалях (Па):
Часто используются внесистемные единицы: нормальная атмосфера (атм) и миллиметр ртутного столба (мм Hg):
Французский ученый Б. Паскаль в середине XVII века эмпирически установил закон, названный законом Паскаля:
Давление в жидкости или газе передается во всех направлениях одинаково и не зависит от ориентации площадки, на которую оно действует.
Для иллюстрации закона Паскаля на рис. 1.15.1 изображена небольшая прямоугольная призма, погруженная в жидкость. Если предположить, что плотность материала призмы равна плотности жидкости, то призма должна находиться в жидкости в состоянии безразличного равновесия. Это означает, что силы давления, действующие на грани призмы, должны быть уравновешены. Это произойдет только в том случае, если давления, т. е. силы, действующие на единицу площади поверхности каждой грани, одинаковы:

|
| Рисунок 1.15.1. Закон Паскаля: |
Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости. Сила давления на дно цилиндрического сосуда высоты
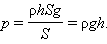 |
Такое же давление на глубине
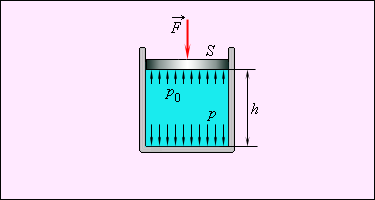
Если жидкость находится в цилиндре под поршнем (рис. 1.15.2), то действуя на поршень некоторой внешней силой 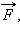 можно создавать в жидкости дополнительное давление
можно создавать в жидкости дополнительное давление
Таким образом, полное давление в жидкости на глубине
Если на рис. 1.15.2 поршень убрать, то давление на поверхность жидкости будет равно атмосферному давлению:
|
| Рисунок 1.15.2. Зависимость давления от высоты столба жидкости |
Из-за разности давлений в жидкости на разных уровнях возникает выталкивающая или архимедова сила 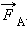
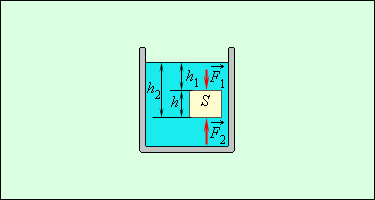
Рис. 1.15.3 поясняет появление архимедовой силы. В жидкость погружено тело в виде прямоугольного параллелепипеда высотой
Поэтому выталкивающая сила 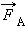 будет направлена вверх, и ее модуль равен
будет направлена вверх, и ее модуль равен
Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемое законом Архимеда, справедливо для тел любой формы.
|
| Рисунок 1.15.3. Архимедова сила. |
Из закона Архимеда вытекает, что если средняя плотность тела
Из выражения для полного давления в жидкости
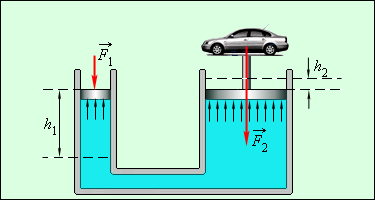
Если оба вертикально расположенных цилиндра сообщающихся сосудов закрыть поршнями, то с помощью внешних сил, приложенных к поршням, в жидкости можно создать большое давление
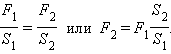 |
Если 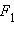 на расстояние
на расстояние 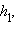 то поршень в широком цилиндре переместится на расстояние
то поршень в широком цилиндре переместится на расстояние 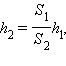 поднимая тяжелый груз.
поднимая тяжелый груз.
Таким образом, выигрыш в силе в 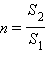 раз обязательно сопровождается таким же проигрышем в расстоянии. При этом произведение силы на расстояние остается неизменным:
раз обязательно сопровождается таким же проигрышем в расстоянии. При этом произведение силы на расстояние остается неизменным:
Это правило выполняется для любых идеальных машин, в которых не действуют силы трения. Оно называется «золотым правилом механики».
|
| Рисунок 1.15.5. Гидравлическая машина. 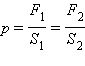 |
Гидравлические машины, используемые для подъема грузов, называются домкратами. Они широко применяются также в качестве гидравлических прессов. В качестве жидкости обычно используются минеральные масла.

 |
|
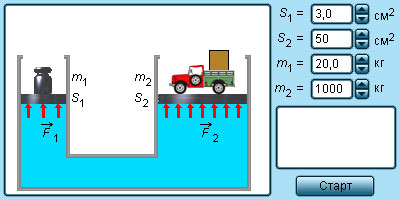
Модель.
Гидравлическая машина
|
 |
 |
 |

