Глава 1. Механика

Задачи с решениямиЗадачи с решениямиВключить/Выключить фоновую музыкуВключить/Выключить звуки событий


Через тяжелый блок массой m = 2 кг перекинута легкая нить, на концах которой подвешены грузы массами m1 = 5 кг и m2 = 4 кг. Считая блок однородным диском, определите ускорение, с которым будут двигаться грузы. Трение не учитывать.

Решение

Изобразим на рис. 1.23.1 силы, действующие на грузы и блок.
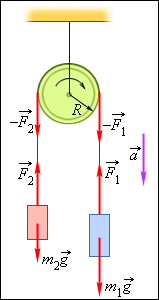Рисунок 1.23.1.

Так как блок обладает массой, натяжения нити F1 и F2 справа и слева от блока неодинаковы. Применим второй закон Ньютона к движущимся грузам:

m1g – F1 = m1a,

m2g – F2 = –m2a.

Применим теперь основное уравнение динамики вращательного движения твердого тела к вращению блока:

(F1 – F2)R = Iε,
где I – момент инерции блока, ε – его угловое ускорение. Момент инерции сплошного диска

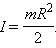
Принимая во внимание, что 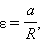уравнение вращательного движения блока можно переписать в виде:

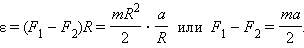
Из двух первых уравнений можно получить:

(m1 – m2)g = (m1 + m2)a + (F1 – F2).

Подставив вместо разности 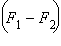выражение 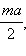получим окончательно:

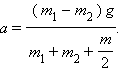
Числовой расчет дает: a = 1 м/с2.


 1 из 2