

 |
 |
Свободным падением тел называют падение тел на Землю в отсутствие сопротивления воздуха (в пустоте). В конце XVI века знаменитый итальянский ученый Г. Галилей опытным путем с доступной для того времени точностью установил, что в отсутствие сопротивления воздуха все тела падают на Землю равноускоренно, и что в данной точке Земли ускорение всех тел при падении одно и то же. До этого в течение почти двух тысяч лет, начиная с Аристотеля, в науке было принято считать, что тяжелые тела падают на Землю быстрее легких.
Ускорение, с которым падают на Землю тела, называется ускорением свободного падения. Вектор ускорения свободного падения обозначается символом 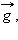 он направлен по вертикали вниз. В различных точках земного шара в зависимости от географической широты и высоты над уровнем моря числовое значение
он направлен по вертикали вниз. В различных точках земного шара в зависимости от географической широты и высоты над уровнем моря числовое значение
Простым примером свободного падения является падение тела с некоторой высоты
Скорость отрицательна, так как вектор скорости направлен вниз.
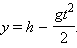 |
Время падения
|
Скорость тела в любой точке составляет:
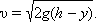 |
В частности, при
|
Пользуясь этими формулами, можно вычислить время падения тела с данной высоты, скорость падения тела в любой момент после начала падения и в любой точке его траектории и т. д.
Аналогичным образом решается задача о движении тела, брошенного вертикально вверх с некоторой начальной скоростью
Через время
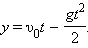 |
Тело возвращается на землю (
Максимальная высота подъема
|
|
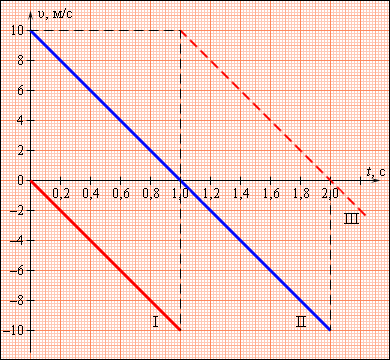
| Рисунок 1.5.1. Графики скоростей для различных режимов движения тела с ускорением |
На рис. 1.5.1 представлены графики скоростей для трех случаев движения тела с ускорением
График II – случай движения тела, брошенного вертикально вверх с начальной скоростью
График III – продолжение графика I. Свободно падающее тело при ударе о землю отскакивает (мячик), и его скорость за очень короткое время меняет знак на противоположный. Дальнейшее движение тела не отличается от случая II.
Задача о свободном падении тел тесно связана с задачей о движении тела, брошенного под некоторым углом к горизонту. Для кинематического описания движения тела удобно одну из осей системы координат (ось 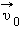 тела и его проекции на координатные оси.
тела и его проекции на координатные оси.
|
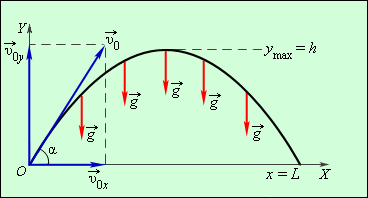
| Рисунок 1.5.2. Движение тела, брошенного под углом 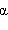 к горизонту. Разложение вектора к горизонту. Разложение вектора 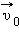 начальной скорости тела по координатным осям начальной скорости тела по координатным осям |
Таким образом, для движения вдоль оси
Приведем здесь некоторые формулы, описывающие движение тела, брошенного под углом
Время полета:
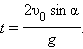 |
Дальность полета:
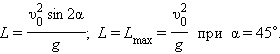 |
Максимальная высота подъема:
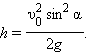 |

 |
|
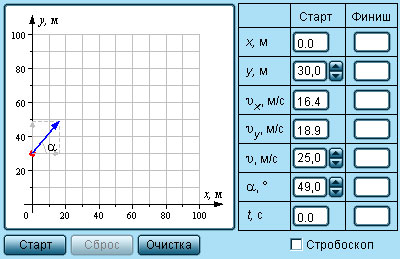
Модель.
Движение тела, брошенного под углом к горизонту
|
Движение тела, брошенного под углом к горизонту, происходит по параболической траектории. В реальных условиях такое движение может быть в значительной степени искажено из-за сопротивления воздуха, которое может во много раз уменьшить дальность полета тела.
 |
 |
 |

