|
|
Рассмотрим два произвольных вектора: 
и
Векторным произведением вектора 
на вектор 
называется третий вектор
который обладает следующими свойствами:
Его длина равна 
Вектор 
перпендикулярен к плоскости, в которой лежат вектора 
и 
Вектор 
направлен так, что поворот от вектора 
к вектору
осуществляется против часовой стрелки, если смотреть из конца вектора 
(в этом случае, говорят, что тройка векторов 
и
– правая).
|
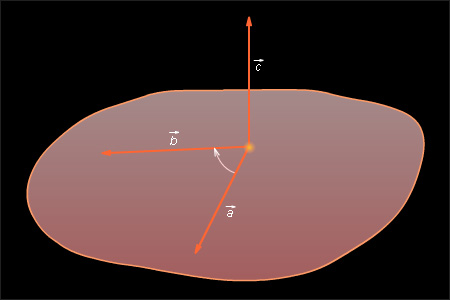
| Рисунок 9.6.1 |
Векторное произведение обозначается квадратными скобками:
 |
векторное произведение произвольного вектора на нулевой вектор равно нулевому вектору;
векторное произведение двух коллинеарных векторов равно нулевому вектору;
координаты векторного произведения 
векторов 
и 
следующие 
|
|
 |
