

 |
 |
Рассмотрим произвольную точку 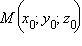 в пространстве и некоторый вектор
в пространстве и некоторый вектор 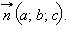 Очевидно, что геометрическим местом точек
Очевидно, что геометрическим местом точек 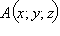 таких, что вектор
таких, что вектор 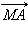 перпендикулярен вектору
перпендикулярен вектору 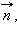 будет плоскость, проходящая через точку
будет плоскость, проходящая через точку 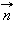 является направляющим. Нашей задачей будет установить уравнение плоскости, то есть найти соотношение, которому удовлетворяют координаты точки
является направляющим. Нашей задачей будет установить уравнение плоскости, то есть найти соотношение, которому удовлетворяют координаты точки
Запишем условие перпендикулярности векторов с использованием скалярного произведения:
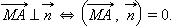 |
Запишем последнее равенство в координатах:
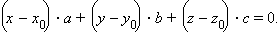 |
Поскольку все наши выкладки были равносильными, то это и есть уравнение плоскости, проходящей через заданную точку. Преобразуем его к виду
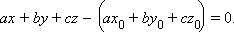 |
Обозначая 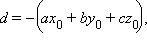 получим
получим
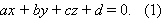 |
Это и есть так называемое общее уравнение плоскости.

Вектор 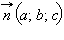 называется нормальным вектором (или просто нормалью) для плоскости, заданной общим уравнением (1).
называется нормальным вектором (или просто нормалью) для плоскости, заданной общим уравнением (1).
Нормальный вектор к плоскости перпендикулярен ей, что следует из самого вывода уравнения плоскости.
Рассмотрим плоскость 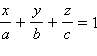 называется уравнением плоскости в отрезках на осях.
называется уравнением плоскости в отрезках на осях.
|
|
|
| Чертеж 9.7.1 |
Эта плоскость пересекает оси
Плоскость, изображенная на чертеже 9.7.1, имеет такое уравнение в отрезках на осях: 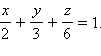
 |
 |
 |

