Глава 3. Основы небесной механики
3.1. Движение в гравитационном поле
3.1.2. Механическая энергия в гравитационном поле
 1 1
|
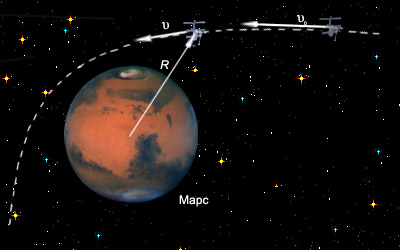
| Рисунок 3.1.2.1. Закон сохранения энергии в гравитационном поле
|
В общем случае невозмущенное движение в гравитационном поле определяется законом сохранения энергии, то есть K + U = сonst, где
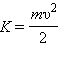 – кинетическая энергия тела массой m, движущегося со скоростью υ,
– кинетическая энергия тела массой m, движущегося со скоростью υ,
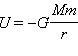 – потенциальная энергия этого тела, находящегося на расстоянии r от тела массой M. Закон сохранения энергии можно переписать в виде:
– потенциальная энергия этого тела, находящегося на расстоянии r от тела массой M. Закон сохранения энергии можно переписать в виде:
Константа h называется постоянной энергии. Она прямо пропорциональна полной механической энергии тела E и зависит только от начального радиус-вектора r0 и начальной скорости υ0. При h < 0 (
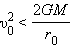 ) кинетической энергии тела недостаточно для преодоления гравитационной связи. Величина радиус-вектора тела ограничена сверху и имеет место обращение по замкнутой, эллиптической орбите. Такое движение можно уподобить движению маятника – тот же самый переход кинетической энергии в потенциальную во время подъема и обратный – при опускании. Подобное движение называется финитным. Для h = 0 (
) кинетической энергии тела недостаточно для преодоления гравитационной связи. Величина радиус-вектора тела ограничена сверху и имеет место обращение по замкнутой, эллиптической орбите. Такое движение можно уподобить движению маятника – тот же самый переход кинетической энергии в потенциальную во время подъема и обратный – при опускании. Подобное движение называется финитным. Для h = 0 (
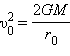 ) при неограниченном возрастании радиус-вектора тела его скорость уменьшается до нуля – это движение по параболе. Оно инфинитно. При h > 0 (
) при неограниченном возрастании радиус-вектора тела его скорость уменьшается до нуля – это движение по параболе. Оно инфинитно. При h > 0 (
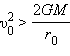 ) кинетическая энергия тела достаточно велика, и на бесконечном расстоянии от притягивающего центра тело будет иметь ненулевую скорость удаления от него – это движение по гиперболе. Тело также может двигаться по прямой. Это происходит, когда его скорость направлена к притягивающемуся центру или от него. Таким образом, можно сказать, что тело движется относительно притягивающего центра только по орбитам, являющимися коническими сечениями.
) кинетическая энергия тела достаточно велика, и на бесконечном расстоянии от притягивающего центра тело будет иметь ненулевую скорость удаления от него – это движение по гиперболе. Тело также может двигаться по прямой. Это происходит, когда его скорость направлена к притягивающемуся центру или от него. Таким образом, можно сказать, что тело движется относительно притягивающего центра только по орбитам, являющимися коническими сечениями.
 2 2
|
| Рисунок 3.1.2.2. Финитное и инфинитное движения
|
Критическая скорость, при которой происходит движение по параболе, называют параболической скоростью. Ее можно определить из закона сохранения энергии:
Таким образом, чтобы навсегда покинуть Землю, тело у поверхности Земли должно иметь скорость не меньше 11,2 км/с. Аналогичная величина для Солнца составляет 618 км/с. Тело, стремящееся навсегда покинуть Солнечную систему и находящееся на орбите Земли, должно иметь скорость не меньше 42,1 км/с.
Приближение тела к притягивающему центру всегда должно сопровождаться увеличением орбитальной скорости тела, а удаление – уменьшением в полном соответствии со вторым законом Кеплера.







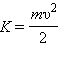
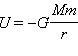
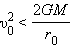 ) кинетической энергии тела недостаточно для преодоления гравитационной связи. Величина радиус-вектора тела ограничена сверху и имеет место обращение по замкнутой, эллиптической орбите. Такое движение можно уподобить движению маятника – тот же самый переход кинетической энергии в потенциальную во время подъема и обратный – при опускании. Подобное движение называется финитным. Для
) кинетической энергии тела недостаточно для преодоления гравитационной связи. Величина радиус-вектора тела ограничена сверху и имеет место обращение по замкнутой, эллиптической орбите. Такое движение можно уподобить движению маятника – тот же самый переход кинетической энергии в потенциальную во время подъема и обратный – при опускании. Подобное движение называется финитным. Для 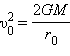 ) при неограниченном возрастании радиус-вектора тела его скорость уменьшается до нуля – это движение по параболе. Оно инфинитно. При
) при неограниченном возрастании радиус-вектора тела его скорость уменьшается до нуля – это движение по параболе. Оно инфинитно. При 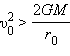 ) кинетическая энергия тела достаточно велика, и на бесконечном расстоянии от притягивающего центра тело будет иметь ненулевую скорость удаления от него – это движение по гиперболе. Тело также может двигаться по прямой. Это происходит, когда его скорость направлена к притягивающемуся центру или от него. Таким образом, можно сказать, что тело движется относительно притягивающего центра только по орбитам, являющимися коническими сечениями.
) кинетическая энергия тела достаточно велика, и на бесконечном расстоянии от притягивающего центра тело будет иметь ненулевую скорость удаления от него – это движение по гиперболе. Тело также может двигаться по прямой. Это происходит, когда его скорость направлена к притягивающемуся центру или от него. Таким образом, можно сказать, что тело движется относительно притягивающего центра только по орбитам, являющимися коническими сечениями.




