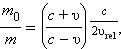Глава 3. Основы небесной механики
3.2. Искусственные спутники Земли
3.2.1. Реактивное движение
В настоящем параграфе говорится о медленном движении тел, масса которых меняется за счет потери или приобретения вещества. Уравнения движения тел с переменной массой являются следствиями законов Ньютона. Тем не менее, они представляют большой интерес, главным образом, в связи с ракетной техникой.
Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты.

 |
|
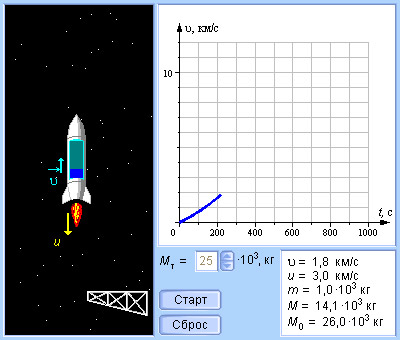
Модель 3.4.
Реактивное движение
|
Принцип действия ракеты очень прост. Ракета с большой скоростью выбрасывает вещество (газы), воздействуя на него с большой силой. Выбрасываемое вещество с той же, но противоположно направленной силой, в свою очередь, действует на ракету и сообщает ей ускорение в противоположном направлении. Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени. На этом положении и основана теория движения ракет.
Несложные преобразования закона изменения импульса приводят к уравнению Мещерского:
Здесь m – текущая масса ракеты,
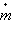 – ежесекундный расход массы, υ – скорость газовой струи (т.е. скорость истечения газов относительно ракеты), F – внешние силы, действующие на ракету. По форме это уравнение напоминает второй закон Ньютона, однако, масса тела m здесь меняется во времени из-за потери вещества. К внешней силе
– ежесекундный расход массы, υ – скорость газовой струи (т.е. скорость истечения газов относительно ракеты), F – внешние силы, действующие на ракету. По форме это уравнение напоминает второй закон Ньютона, однако, масса тела m здесь меняется во времени из-за потери вещества. К внешней силе
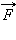 добавляется дополнительный член
добавляется дополнительный член
 , который может быть истолкован как реактивная сила.
, который может быть истолкован как реактивная сила.
Применив уравнение Мещерского к движению ракеты, на которую не действуют внешние силы, и проинтегрировав уравнение, получим формулу Циолковского:
Релятивистское обобщение этой формулы имеет вид
где c – скорость света. При малых скоростях v оно переходит в формулу Циолковского.
Формула Циолковского позволяет рассчитать запас топлива, необходимый, чтобы сообщить ракете скорость υ. В частности, можно получить, что запас топлива, необходимого для осуществления межзвездного путешествия (с возвращением обратно), должен превышать массу космического корабля в несколько тысяч раз. Но для межзвездных перелетов ракеты на химическом топливе абсолютно непригодны. Расстояния до звезд измеряются световыми годами – от ближайшей звезды свет идет до Земли около 4 лет. Поэтому для достижения даже ближайших звезд нужны космические корабли, скорости которых близки к скорости света c. Если, например, скорость ракеты должна составлять четверть скорости света, то на каждую тонну полезного груза должно приходиться 5∙103327 тонн топлива! (Кстати, при таких скоростях применима только релятивистская формула Циолковского; она еще больше увеличивает необходимое количество топлива). Обычно, когда имеют дело с очень большими величинами, их называют «астрономическими». В данном случае такое сравнение не годится – речь идет о величинах несравненно большего масштаба. Вряд ли имеет смысл говорить о движении столь фантастически гигантского космического корабля относительно Вселенной, имеющей по сравнению с ним ничтожную массу.
Было бы неосторожно на основании вышеизложенного сделать вывод, что звездные миры никогда не будут доступны земным космонавтам. Только отдаленное будущее покажет, возможно это или нет. Для превращения ракеты в звездолет, прежде всего, необходимо повысить скорость струи, приблизив ее к скорости света. Идеальным был бы случай u = c. Так было бы в фотонной ракете, в которой роль газовой струи должен был бы играть световой пучок. Реактивная сила в фотонной ракете осуществлялась бы давлением света. Превращение вещества в излучение постоянно происходит внутри звезд. Этот процесс осуществляется и на Земле (взрывы атомных и водородных бомб). Возможно ли придать ему управляемый характер и использовать в фотонных ракетах – на этот вопрос отвечать сейчас преждевременно.








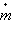 – ежесекундный расход массы,
– ежесекундный расход массы, 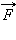 добавляется дополнительный член
добавляется дополнительный член
 , который может быть истолкован как реактивная сила.
, который может быть истолкован как реактивная сила.