Глава 3. Основы небесной механики

3.2. Искусственные спутники Земли

3.2.3. Космическое маневрирование

Маневры космических аппаратов необходимы во многих случаях:

• для сближения с другим космическим аппаратом или коррекции траектории при подлете к планете назначения;
• для поддержания постоянной высоты полета при движении в верхних слоях атмосферы;
• для изменения периода обращения, необходимого, например, при стыковке;
• при посадке космического аппарата.

Рассмотрим основы теории эволюции орбит.

Пусть спутник двигается по эллиптической орбите. Мгновенный импульс не меняет координат, а меняет лишь скорость. Поэтому произойдет мгновенное изменение большой полуоси, т.е. переход с орбиты 1 на орбиту 2.

1

Рисунок 3.2.3.1. На схемах приведено изменение первоначально круговых орбит импульсами, направленными «по скорости» и «против скорости». Как видно из схем, орбита испытывает наибольшее геометрическое смещение в области, противолежащей точке, в которой телу был сообщен импульс

2

Рисунок 3.2.3.2. Торможение КА в атмосфере

Торможение в разреженной атмосфере можно моделировать мгновенными импульсами в перицентре, благодаря чему уменьшается длина большой полуоси орбиты. В результате эллиптическая орбита с каждым оборотом все больше и больше приближается к окружности. Когда вся орбита окажется в атмосфере (критическая высота – около 100 км), торможение будет настолько велико, что спутник упадет на Землю.

Торможение в атмосфере используется при посадке космических аппаратов. Достаточно «столкнуть» спутник до высоты около 100 км (требуемый импульс – около 100 м/с), после чего он сам будет тормозиться за счет взаимодействия с атмосферой.

Двухимпульсный переход необходим в тех случаях, когда исходная и требуемая орбита не имеют общих точек – например, перелет от одной планеты к другой. Для такого перелета необходимо сообщить два импульса, а промежуточная орбита называется эллипсом Гомана.

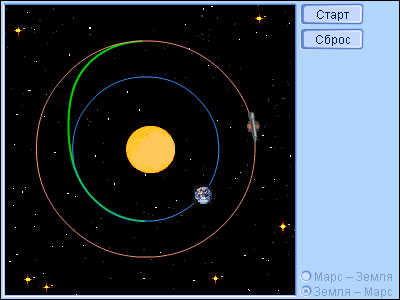
Модель 3.7. Межпланетный перелет

Изменение формы орбиты является весьма экономным маневром. Так, импульс в 140 м/с, которого хватило бы для поворота орбиты на лишь 1°, способен изменить высоту полета на 240 км.

Одним из самых «дорогих» в смысле затрат топлива маневров является маневр изменения плоскости орбиты. Чтобы изменить наклонение на один радиан, требуется, как минимум, первая космическая скорость! Рассчитывая движение космических аппаратов, стараются обходиться без этих маневров, ожидая, пока Земля сама повернется на нужный угол.

3

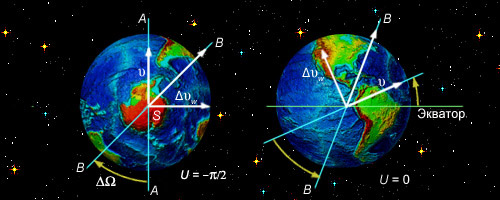Рисунок 3.2.3.3. Эффективность маневра изменения плоскости орбиты зависит от того, в какой точке орбиты он выполняется

Эффективность этого маневра зависит от того, в какой точке орбиты он выполняется: включение двигателей в узле орбиты приведет к изменению наклонения, в то время, как импульс в точке, широта которой равна π/2, оставит наклонение прежним, но изменит долготу восходящего узла.

Скорость космического аппарата описывается формулой , где M – масса притягивающего центра, r – расстояние до него, a – большая полуось орбиты. Из этой формулы легко получить, что затраты энергии на межпланетные перелеты слабо зависят от a, т.к. слагаемое r/a приближается к нулю (особенно для дальних перелетов). Поэтому необходимые скорости разгона для путешествия к Луне и к Марсу имеют одинаковые порядки, а их различие связано, прежде всего, с необходимостью учитывать движение вокруг Солнца.

4

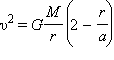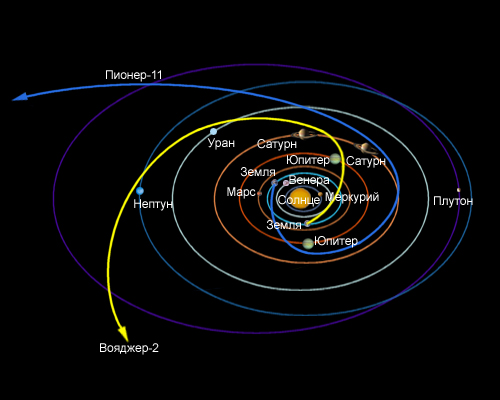Рисунок 3.2.3.4. Межпланетный перелет

При путешествии на другую планету необходима скорость не менее 11 км/с, после чего космический аппарат выходит на эллиптическую орбиту вокруг Солнца. При подлете к планете включаются двигатели торможения, после чего аппарат выходит на околопланетную орбиту или садится на поверхность планеты.

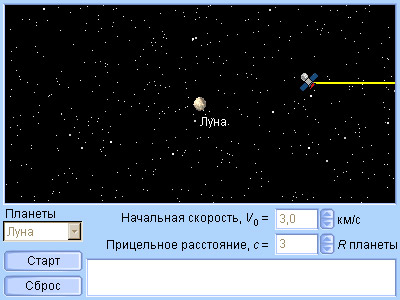
Модель 3.8. Гравитационный маневр

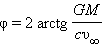
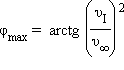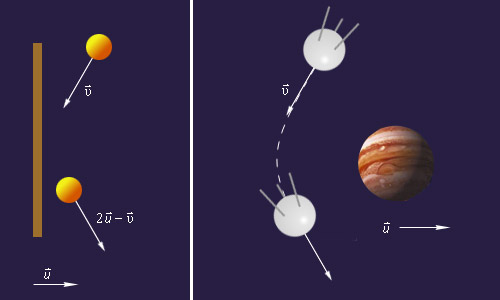Для дополнительного разгона используется гравитационное поле планет, мимо которых пролетает космический аппарат, – осуществляется гравитационный маневр. Аппарат войдет в грависферу планеты вдоль асимптоты со скоростью υ_∞ относительно планеты, повернется на угол (здесь c – прицельная дальность – расстояние между прямой, параллельной вектору скорости аппарата в бесконечности и центром планеты) и выйдет из ее поля действия со той же по модулю относительно планеты скоростью υ_∞ (закон сохранения импульса). Максимальный угол поворота достигается при прицельной дальности, равной радиусу планеты: , где υ_I – первая космическая скорость, свойственная данной планете.

5

Рисунок 3.2.3.5. Принцип гравитационного маневра похож на обычное упругое отражение тела от массивной стенки