Глава 3. Основы небесной механики

3.2. Искусственные спутники Земли

3.2.2.1. Орбитальные элементы

Движение спутника будет определено в пространстве, если известны плоскость, в которой лежит его орбита, размеры и форма этой орбиты, ее ориентация в пространстве и момент времени, в который спутник находится в определенной точке орбиты. В качестве примера рассмотрим движение спутника вокруг Земли.

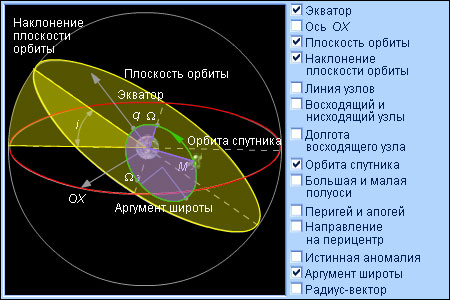
Модель 3.6. Элементы орбиты спутника

Чтобы охарактеризовать ориентацию орбиты в пространстве, нужно прежде всего задать базовую систему координат, начало которой совпадает с фокусом орбиты O (т. е. с центром Земли). За основную плоскость OXY, относительно которой определяется положение орбиты спутника, принимается плоскость экватора. Ось OX пересекает экватор в точке с долготой 0º, соответствующей Гринвичскому меридиану. Для задач, связанных с межпланетными перелетами, обычно выбирают плоскость эклиптики, а ось OX направлена на точку весеннего равноденствия.

Плоскость орбиты пересекается с экватором в двух точках. Точка Ω перехода из южного полушария в северное называется восходящим узлом. Противоположная ей точка Ω' называется нисходящим узлом. Угол Ω между осью OX и направлением на восходящей узел OΩ называется долготой восходящего узла. Долгота восходящего узла измеряется в пределах от 0° до 360°. Если орбита лежит в плоскости экватора, то понятие восходящего узла считается неопределенным. Прямая, по которой плоскость орбиты пересекается с базовой плоскостью OXY, называется линией узлов.

Угол i между плоскостью экватора и плоскостью траектории небесного тела называется наклонением плоскости орбиты. Он принимает значение от 0° до 180°. Если 0° < i < 90°, то спутник вращается в том же направлении, что и Земля. Такое движение называется прямым. Понятно, что при одноимпульсном выведении на орбиту наклонение не может быть меньше широты точки старта (для российских спутников, запускаемых с космодрома Байконур, эта величина составляет 46,5°).

Если из точки O провести прямые в перицентр q и в мгновенное положение небесного тела M, то соответствующие углы, отсчитываемые в плоскости орбиты, будут: Ω – угловое расстояние перицентра от узла и ν – истинная аномалия. Оба угла могут изменяться от 0° до 360°. Часто рассматривают сумму этих углов u = ω + ν, называющуюся аргументом широты.

Иногда к описанным элементам добавляют эпоху τ – время прохождения через перицентр.

1

Рисунок 3.2.2.1.1. Благодаря вращению Земли с космического аппарата за короткое время можно увидеть большую часть поверхности земного шара. Карта Центра управления полетом (ЦУП)

Углы Ω и i полностью определяют плоскость орбиты, большая полуось a и эксцентриситет e – форму этой орбиты. Направление на перицентр ω задает ориентацию орбиты на плоскости, а широта u (либо истинная аномалия ν, либо, наконец, эпоха τ) – положение тела на этой орбите.

С каждым оборотом долгота восходящего узла Ω меняется. Это вызвано вращением Земли. Если бы космический аппарат двигался в поле однородного шара, то остальные элементы орбиты не изменялись бы (за исключением, конечно, истинной аномалии). Однако возмущения, вызванные гравитационным полем Солнца и Луны, атмосферой и прочими причинами изменяют движение спутника. Важнейшим из этих возмущений для орбит, близких к Земле, является возмущение, вызванное несферичностью Земли.

2

Рисунок 3.2.2.1.2. Качественная интерпретация прецессии орбиты спутника в поле несферичной Земли

Так как Земля сплюснута к экватору, ее гравитационное поле отличается от поля однородного шара. Качественную интерпретацию вносимого возмущения можно получить, «размазав» космический аппарат по орбите. Дополнительная масса на экваторе заставляет орбиту прецессировать так же, как сила тяжести заставляет прецессировать наклонившуюся ось быстро вращающегося волчка. Благодаря указанной прецессии долгота восходящего узла, например, станции «Мир» дополнительно смещалась на 4° в сутки (около 400 км).

Прецессия орбиты в некоторых случаях может оказаться весьма полезна. В частности, она помогает получить карты звездного неба. Если телескоп на орбите направлен всегда по вертикали от центра Земли, то за один виток можно сфотографировать звезды узкой кольцевой зоны около плоскости орбиты. Если бы прецессии орбиты не существовало, то космический аппарат фотографировал бы одни и те же звезды. А благодаря указанной прецессии все небесная сфера могла бы быть отснята за 45 суток без дополнительных затрат энергии на изменение плоскости спутника.

Несферичность Земли изменяет также направление на перицентр ω.

Если спутник постоянно находится над одной и той же точкой земного шара, то орбита, по которой он движется, называется геостационарной. Ее высоту можно легко найти из второго закона, приравняв угловую скорость вращения Земли к угловой скорости спутника. Она равна
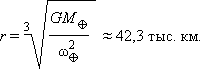