Глава 3. Основы небесной механики
Задачи с решениями
Межпланетный космический корабль выведен на промежуточную орбиту вокруг Земли. В какой точке орбиты выгоднее включить двигатели для разгона до второй космической скорости?
РешениеПусть Vпер1 – первая космическая скорость в перигее, Vпер2 – вторая космическая скорость в перигее, Vап1 – первая космическая скорость в апогее, Vап2 – вторая космическая скорость в апогее. Vпер и Vап – скорости корабля в перигее и апогее при движении по эллиптической орбите, Rпер и Rап – расстояния перигея и апогея от центра Земли.
Расстояние в перигее Rпер = a∙(1 – e), расстояние в апогее Rап = a∙(1 + e)
Rап/Rпер = (1 + e)/(1 – e).
По второму закону Кеплера сравним площади двух малых треугольников в перигее и в апогее, заметаемых за одинаковое время Δτ: 1/2∙Vпер∙a∙(1 – e)∙Δτ = 1/2∙Vап∙a∙(1 + e)∙Δτ;
VперRпер = VапRап.
Из закона сохранения энергии
e = 1 – (Vап/Vап1)2 = (Vпер/Vпер1)2 – 1.
e = 1 – 2(Vап/Vап2)2 = 2(Vпер/Vпер2)2 – 1.
Удельный импульс, который необходим космическому кораблю до достижения второй космической скорости в перигее:
ΔVпер = Vпер2 – Vпер.
Удельный импульс, который необходим космическому кораблю до достижения второй космической скорости в апогее:
ΔVап = Vап2 – Vап.
Отсюда ΔVпер = A ∙ ΔVап, где коэффициент А зависит только от эксцентриситета:
При эллиптической орбите 0 < e < 1, A > 1.
Следовательно, ΔVпер < ΔVап, разгон космического корабля в районе перигея требует меньших затрат энергии, чем разгон в области апогея.
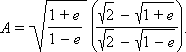
9 из 9
 |
