Глава 1. Теоретические сведения о функциях
1.1. Числовые последовательности
1.1.2. Свойства сходящихся последовательностей
Последовательность {xn} называется ограниченной снизу (сверху), если существует такое число C, что все члены последовательности удовлетворяют условию xn ≥ C (xn ≤ C). Последовательность, ограниченную как сверху, так и снизу, называют ограниченной.
 1
|
| Рисунок 1.1.2.1. Последовательность называют ограниченной, если C1 ≤ xn ≤ C2.
|
Геометрически ограниченность последовательности означает, что все ее значения лежат на некотором отрезке.
Можно показать, что если последовательность имеет предел, то она ограничена.
Заметим, что не всякая ограниченная последовательность является сходящейся. Примером расходящейся ограниченной последовательности может служить последовательность {xn}: xn = (–1)n.
Теорема о трех последовательностях. Если последовательности {
xn}, {
yn}, {
zn} таковы, что
xn ≤
yn ≤
zn для всех
n ≥ N, и
то последовательность {
yn} сходится, и
Если
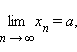
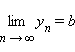 и для любого
и для любого
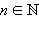
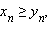 то a ≥ b.
то a ≥ b.
Любая неубывающая ограниченная сверху последовательность сходится.
Любая невозрастающая ограниченная снизу последовательность сходится.
Суммой, разностью, произведением и частным двух последовательностей {xn} и {yn} называют соответственно последовательности {xn + yn}, {xn – yn}, {xn ∙ yn}, {xn / yn}. При определении частного предполагается, что yn ≠ 0 при всех n.
Справедлива следующая теорема (основная теорема теории пределов): если
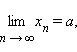
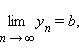 то:
то:
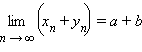 ;
;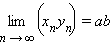 ;
;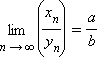 при условии, что b ≠ 0 и
при условии, что b ≠ 0 и  для всех n.
для всех n.
Последовательность {αn} называется бесконечно малой, если
Если число a – предел последовательности {xn}, то последовательность {αn}, где αn = xn – a, бесконечно малая. Примером бесконечно малой последовательности является геометрическая прогрессия {qn}, где |q| < 1.
- Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.
- Из определения бесконечно малой последовательности непосредственно следует, что алгебраическая сумма конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Заметим, что конечность числа бесконечно малых последовательностей в этой алгебраической сумме существенна.
- Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Заметим, что и здесь конечность числа последовательностей также существенна, т. к. произведение бесконечного числа бесконечно малых последовательностей может уже и не быть бесконечно малой последовательностью.
Множества 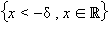 и
и 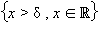 называются δ-окрестностями –∞ и +∞ соответственно.
называются δ-окрестностями –∞ и +∞ соответственно.
Определим понятие бесконечного предела. Говорят, что
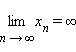 , если для любого R > 0 существует
, если для любого R > 0 существует 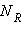 такой, что
такой, что 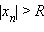 при
при 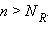
Последовательность {xn} называется бесконечно большой, если
Другими словами, 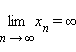 , если для любого δ > 0 найдется номер
, если для любого δ > 0 найдется номер 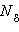 такой, что для любого
такой, что для любого
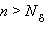
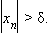 Аналогично вводятся понятия бесконечных пределов +∞ и –∞. Примерами бесконечно больших последовательностей могут служить {n2} или {1 – n}.
Аналогично вводятся понятия бесконечных пределов +∞ и –∞. Примерами бесконечно больших последовательностей могут служить {n2} или {1 – n}.
 2
|
| Рисунок 1.1.2.2. δ-окрестность +∞
|








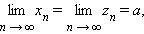
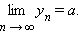
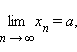
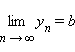
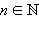
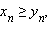 то
то 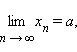
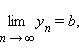
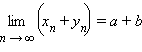
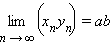
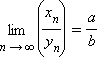
 для всех
для всех 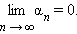
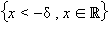 и
и 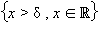 называются δ-окрестностями –∞ и +∞ соответственно.
называются δ-окрестностями –∞ и +∞ соответственно.
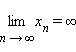
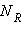 такой, что
такой, что 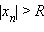 при
при 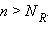
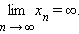
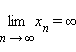
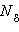 такой, что для любого
такой, что для любого
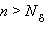
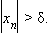 Аналогично вводятся понятия бесконечных пределов +∞ и –∞. Примерами бесконечно больших последовательностей могут служить {
Аналогично вводятся понятия бесконечных пределов +∞ и –∞. Примерами бесконечно больших последовательностей могут служить {




