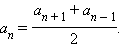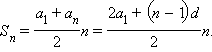Глава 1. Теоретические сведения о функциях
1.1. Числовые последовательности
1.1.3. Арифметическая прогрессия
Числовую последовательность {an}, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d, называют арифметической прогрессией. Число d называется разностью арифметической прогрессии:
Так как an – 1 = an – d, то an + 1 + an – 1 = 2an. Верно и обратное.
Последовательность 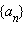 является арифметической тогда и только тогда, когда для любого n > 1
выполняется рекуррентное соотношение
является арифметической тогда и только тогда, когда для любого n > 1
выполняется рекуррентное соотношение
Формула общего члена арифметической прогрессии {an} такова:
Докажем это пользуясь методом математической индукции. Легко убедиться, что для n = 1 данная формула верна. Пусть эта формула верна для n = k. Докажем ее справедливость для n = k + 1. Имеем ak + 1 = ak + d = a1 + (k – 1) · d + d = a1 + k · d. Теорема доказана.
|

 |
|
Модель 1.1.
Растущее дерево
|
Сумма n первых членов арифметической прогрессии {an} равна
Обе формулы легко доказать, используя метод математической индукции. Выполните это самостоятельно.







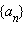 является арифметической тогда и только тогда, когда для любого
является арифметической тогда и только тогда, когда для любого