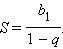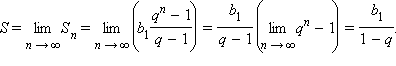Глава 1. Теоретические сведения о функциях
1.1. Числовые последовательности
1.1.4. Геометрическая прогрессия
Числовую последовательность {bn}, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q ≠ 0, называют геометрической прогрессией:
Важно отметить, что число q, которое называется знаменателем прогрессии, отлично от нуля. Так как 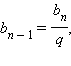 то
то
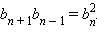 Верна и обратная теорема.
Верна и обратная теорема.
Последовательность {bn} является геометрической тогда и только тогда, когда для любого n > 1
выполняется соотношение
где
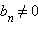
при всех
n. Тем не менее, важно понимать, что формула
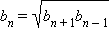
справедлива только для геометрической прогрессии с положительными членами, а предыдущее соотношение верно для произвольной геометрической прогрессии.
Каждый член геометрической прогрессии {bn} определяется формулой
Докажем это пользуясь методом математической индукции. Легко убедиться, что при n = 1 данная формула верна. Пусть эта формула верна для n = k. Докажем ее справедливость для n = k + 1. Имеем bk + 1 = bk · q = b1 · qk – 1 · q = b1 · qk. Теорема доказана.
|

 |
|
Модель 1.2.
Банковский счет
|
Сумма n первых членов геометрической прогрессии {bn} равна
при q ≠ 1 и
Sn = n · b1 при q = 1.
Эти формулы также доказываются методом математической индукции. Докажите их самостоятельно.
При |q| < 1 ,
поэтому в этом случае геометрическая прогрессия называется бесконечно убывающей. Суммой бесконечно убывающей геометрической прогрессии называется число
,
поэтому в этом случае геометрическая прогрессия называется бесконечно убывающей. Суммой бесконечно убывающей геометрической прогрессии называется число
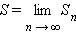 , ,
|
где Sn – сумма n первых членов геометрической прогрессии.
Сумма бесконечно убывающей геометрической прогрессии (|q| < 1) равна
Для доказательства достаточно заметить, что
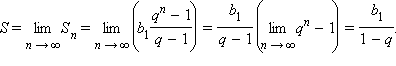 В предпоследнем переходе использовались свойства пределов последовательностей.
В предпоследнем переходе использовались свойства пределов последовательностей.

 |
|
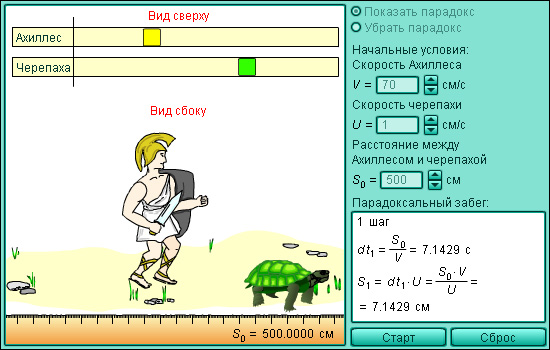
Модель 1.3.
Ахиллес и черепаха
|






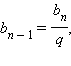 то
то
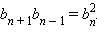

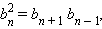
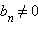 при всех
при всех 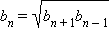 справедлива только для геометрической прогрессии с положительными членами, а предыдущее соотношение верно для произвольной геометрической прогрессии.
справедлива только для геометрической прогрессии с положительными членами, а предыдущее соотношение верно для произвольной геометрической прогрессии.


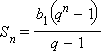
 ,
,
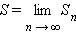 ,
,