Глава 1. Теоретические сведения о функциях
1.2. Системы координат
1.2.1. Декартова система координат
Системой координат называется совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат – и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат. В конкретной невырожденной координатной системе каждой точке соответствует один и только один набор координат.
Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной). Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется ортонормированной (декартовой) системой координат (в честь французского математика Рене Декарта).
|
|
| График 1.2.1.1. Декартова система координат
|
В элементарной математике чаще всего рассматривается двухмерная или трехмерная декартова система координат; координаты обычно обозначаются латинскими буквами x, y, z и называются, соответственно, абсциссой, ординатой и аппликатой. Координатная ось OX называется осью абсцисс, ось OY – осью ординат, ось OZ – осью аппликат. Положительные направления отсчета по каждой из осей обозначаются стрелками.
|
|
| График 1.2.1.2. Координаты точки в декартовой системе координат. Важно отметить, что порядок записи координат существенен; так, например, точки A (–3; 2) и B (2; –3) – это две совершенно различные точки
|
Как определить координаты точки в декартовой системе координат? Проведем через точку A прямые (в трехмерном случае – плоскости), перпендикулярные осям. Расстояния от точек пересечения построенных прямых (плоскостей) с осями абсцисс, ординат (аппликат) до начала координат, взятые со знаком «+», если точки лежат на положительных полуосях, и со знаком «–», если они лежат на отрицательных полуосях, и будут координатами точки A. Координаты точки записываются в скобках: например, A (–3; 2) или B (x0; y0). В трехмерном пространстве координаты точки в декартовой системе координат записываются тремя числами, например, C (5; 0,2; –6).
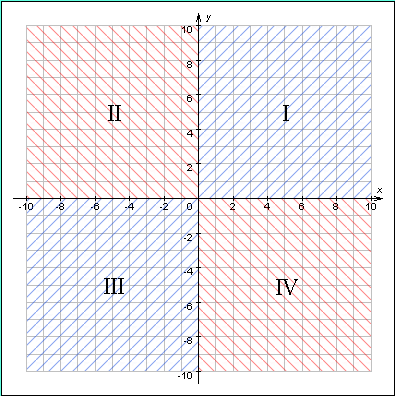 1
|
| Рисунок 1.2.1.1. Координатные оси делят координатную плоскость на четыре квадранта (четверти). Точки, лежащие на осях координат, не принадлежат ни одному квадранту
|
В двухмерной системе координат все точки, лежащие над (под) осью OX, образуют верхнюю (нижнюю) координатную полуплоскость. Все точки, лежащие правее (левее) оси OY образуют правую (левую) координатную полуплоскость.

 |
|
Модель 1.5.
Расстояние между городами
|
В конце этого параграфа приведем некоторые очевидные формулы.
- Расстояние от точки A (x0; y0) до оси OX равно |y0|.
- Расстояние от точки A (x0; y0) до оси OY равно |x0|.
- Расстояние от точки
 до начала координат равно
до начала координат равно

- Расстояние |AB| между точками A (x1; y1) и B (x2; y2) равно

- Точка M, которая является серединой отрезка AB, где A (x1; y1) и B (x2; y2), имеет координаты

|
|
| График 1.2.1.3. Координаты середины отрезка
|
На случай трехмерного пространства эти формулы обобщаются следующим образом:
- Расстояние от точки A (x; y; z) до плоскости OYZ равно |x|.
- Расстояние от точки A (x; y; z) до начала координат равно

- Расстояние |AB| между точками A (x1; y1; z1) и B (x2; y2; z2) равно

- Координаты точки M, которая является серединой отрезка AB, где A (x1; y1; z1) и B (x2; y2; z2) равны










 до начала координат равно
до начала координат равно










