Глава 1. Теоретические сведения о функциях

1.4. Преобразование графиков функций

1.4.4. Алгебраические операции над функциями

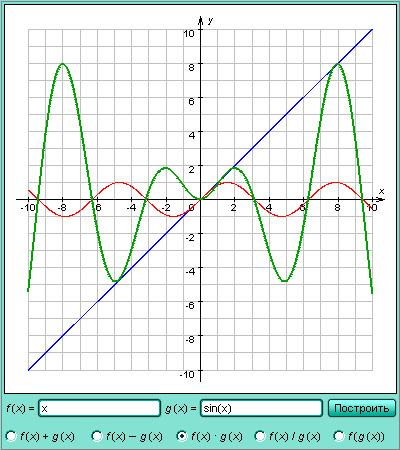
Построение графика суммы (произведения) двух функций производится сложением (умножением) ординат точек графиков с одинаковыми абсциссами. Приведем для примера графики функций y = x + sin x и y = x sin x, являющихся соответственно суммой и произведением графиков y = x и y = sin x.

Правило построения графика функции 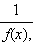если график функции 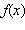уже построен.

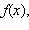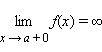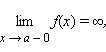• Если x = a – вертикальная асимптота графика функции то есть или то 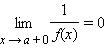или соответственно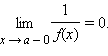
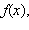
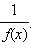
  Таким образорм, в случае, когда x = a – двусторонняя вертикальная асимптота графика функции  x = a будет нулем функции

• Если у графика функции 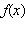есть горизонтальная асимптота 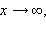y = 0 при то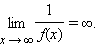

• Если у графика функции 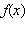есть горизонтальная асимптота 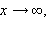y = b при то график функции 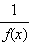будет иметь горизонтальную асимптоту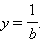

• Если график функции 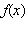пересекает ось абсцисс в точке 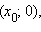то есть 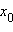– нуль функции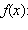 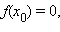  то 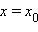– вертикальная асимптота графика функции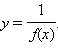

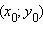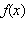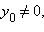• Если точка – точка максимума (минимума) функции и то 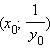– точка минимума (максимума) функции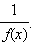

• Промежуткам возрастания (убывания) графика функции 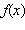соответствуют промежутки убывания (возрастания) графика функции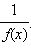

График 1.4.4.2. Графики функци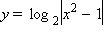й и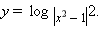

Модель 1.17. Калькулятор функций

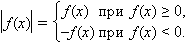
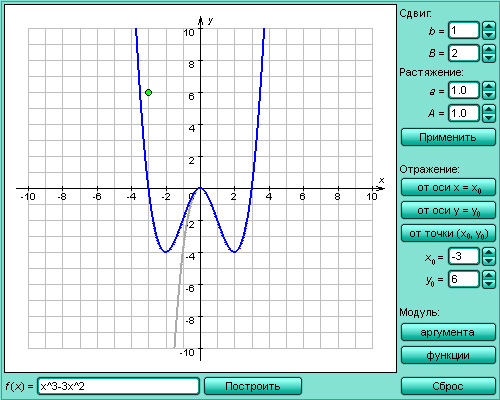
Пусть известен график y = f (x) и нужно построить график функции y = |f (x)|. По определению, Значит, часть графика, лежащую в верхней координатной полуплоскости, изменять не надо, а часть графика, лежащую в нижней координатной полуплоскости, нужно отобразить симметрично оси OX.

Модель 1.16. Преобразование графиков функций

Пусть известен график y = f (x) и нужно построить график функции y = f (|x|). Заметим, что при x ≥ 0  f (|x|) = f (x), а функция y = f (|x|) четная. Поэтому, чтобы построить график функции y = f (|x|), нужно часть графика функции y = f (x), лежащую в левой координатной полуплоскости, отбросить, а часть графика, лежащую в правой координатной полуплоскости, отобразить симметрично относительно оси OY.

График 1.4.4.3. Множество точек, удовлетворяющее уравнению |y| = sin x + 0,5.

Равенство |y| = f (x) не задает функции, так как при f (x) > 0 существуют два значения y = ± f (x), удовлетворяющие ему. Множество точек, задаваемое уравнением |y| = f (x), рисуется следующим образом: строится график функции f (x), отбрасывается его часть, находящаяся ниже оси абсцисс, оставшаяся часть дополняется своим симметричным отражением относительно оси абсцисс.