Глава 2. Элементарные функции и их графики
2.1. Линейная функция
2.1.1. Прямая пропорциональность
Рассмотрим следующую задачу. Мотоцикл движется со скоростью 50 км/ч. Построить график зависимости расстояния, пройденного автомобилем, от времени за первые 6 часов движения.
Поместим сведения о движении мотоцикла в таблицу.
| t, час |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| S (t), км |
0 |
50 |
100 |
150 |
200 |
250 |
300 |
|
| Таблица 2.1.1.1 |
|
|
| График 2.1.1.1. График зависимости пути, пройденного мотоциклом, от времени
|
Построим по этой таблице график функции y = S (t). Точки, описанные в таблице, лежат на одной прямой y = 50 t (км). Если мы хотим узнать путь мотоцикла за 3,5 часа, найдем на оси абсцисс точку t = 3,5, восстановим к этой оси перпендикуляр из данной точки. Он пересечет график функции в точке A. Спроецировав точку A на ось ординат, получим путь, равный 175 км.
В рассмотренной задаче, как и во многих других случаях, встречается ситуация, когда одна величина изменяется пропорционально другой. Так, длина окружности изменяется пропорционально ее радиусу: l = 2πR, площадь прямоугольника с постоянной шириной b пропорциональна длине прямоугольника: S = a · b, путь при равномерном движении пропорционален времени. В таких случаях мы имеем дело с функцией
называемой прямой пропорциональностью. Графиком этой функции является прямая, проходящая через начало координат и не совпадающая с осью OY. Число k называется наклоном или угловым коэффициентом прямой.
Рассмотрим k > 0 и выберем на графике y = kx точку A (1; k). Пусть α – угол, образованный графиком с положительным направлением оси OX (его называют углом наклона прямой). Из прямоугольного треугольника OAB (см. рисунок) имеем, что
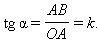
|
|
| График 2.1.1.2. Прямая пропорциональность
|
|
|
| График 2.1.1.3. Определение угла наклона прямой
|
Если же k < 0, то график функции y = kx образует с положительным направлением оси абсцисс тупой угол β. Выберем на графике точку A (1; k) Из теоремы о смежных углах следует, что α = 180º – β. Следовательно,
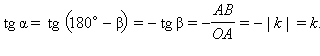 Наконец, если k = 0, то угол α также равен нулю. Таким образом доказана следующая теорема.
Наконец, если k = 0, то угол α также равен нулю. Таким образом доказана следующая теорема.
Тангенс угла наклона прямой относительно оси абсцисс y = kx равен угловому коэффициенту k.