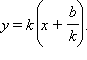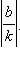Глава 2. Элементарные функции и их графики

2.1. Линейная функция

2.1.2. Линейная функция

Функция

y = kx + b

называется линейной функцией. Ее график получается путем параллельного переноса графика функции y = kx на b вверх, если b > 0, и на |b| вниз, если b < 0. Кроме того, если k ≠ 0, то 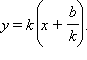Значит, график функции y = kx + b получится из графика y = kx сдвигом на

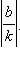
Графики всех линейных функций, имеющих один и тот же угловой коэффициент, параллельны друг другу. Графики функций, коэффициенты k₁ и k₂ которых связаны соотношением k₁k₂ = –1, перпендикулярны друг другу.

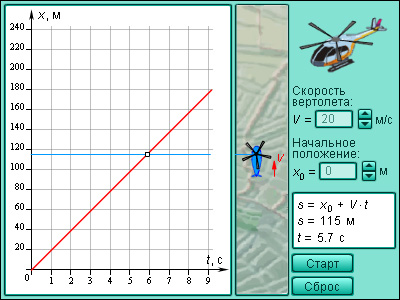
Модель 2.2. Движение с постоянной скоростью

График линейной функции является прямой. Его можно построить несколькими способами.

1. По двум точкам. Выберем произвольные (удобные для построения) значения абсцисс x₁ и x₂, найдем соответствующие им ординаты y₁ = k x₁ + b, y₂ = k x₂ + b. Построим на координатной плоскости точки (x₁; y₁), (x₂; y₂) и проведем через них прямую. Это и будет искомый график.
2. По пересечениям с осями. Решим уравнение y = k x + b, подставив в него сначала x₁ = 0, а затем y₂ = 0. Получим две точки (0; y₁), (x₂; 0). Построим их на координатной плоскости и проведем через них прямую.
3. По угловому коэффициенту. Построим на координатной плоскости произвольную точку прямой. Проведем через эту точку прямую, образующую с осью OX угол, тангенс которого равен k.

Модель 2.3. Способы построения прямой