Глава 1. Теоретические сведения о функциях
1.4. Преобразование графиков функций
1.4.3. Отражение относительно осей и точек
Пусть имеется график функции y = f (x). Чтобы получить график функции, симметричный данному относительно оси OX, нужно умножить значение функции в каждой точке области определения на –1. Алгебраически это задается системой:
Графики функций y = f (x) и y = –f (x) симметричны относительно оси абсцисс.
Аналогичным образом отражается график относительно оси OY:
Графики функций y = f (x) и y = f (–x) симметричны относительно оси ординат.
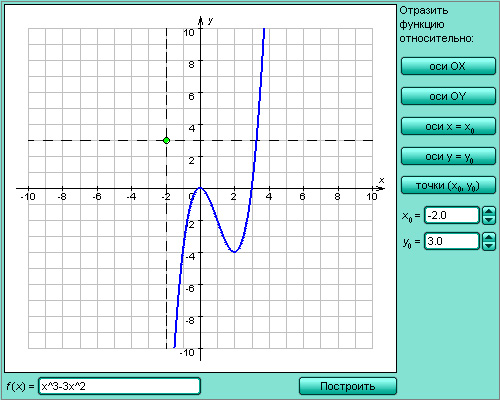
Отражение графика относительно начала координат сводится к отражению сначала относительно оси абсцисс, затем относительно оси ординат и задается системой уравнений

 |
|
Модель 1.15.
Отражение графиков относительно осей и точек
|
Симметричными относительно начала координат являются графики функций y = f (x) и y = –f (–x). Более сложным является вопрос о симметрии графиков относительно произвольных вертикальных и горизонтальных осей. Справедливы следующие утверждения.
- Графики функций y = f (x) и y = 2b – f (x) симметричны относительно горизонтальной оси y = b.
- Графики функций y = f (x) и y = f (2a – x) симметричны относительно вертикальной оси x = a.
Системы уравнений, соответствующие этим преобразованиям, выглядят так:
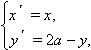 и
и
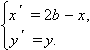 |
Наконец, отражение графика относительно произвольной точки (a, b) задается сначала отражением относительно горизонтальной оси y = b, затем отражением относительно вертикальной оси x = a:
Графики функций y = f (x) и y = 2b – f (2a – x) симметричны относительно точки (a; b).






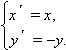
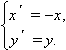
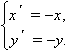


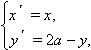 и
и