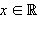Глава 2. Элементарные функции и их графики
2.4. Другие элементарные функции
2.4.5. Гиперболические функции
Функция
называется гиперболическим синусом. Функция
называется гиперболическим косинусом.
Подобно тому, как тригонометрические синус и косинус являются координатами точки на координатной окружности, гиперболические синус и косинус являются координатами точки на гиперболе.
Эти функции определены и непрерывны на всей числовой оси. Гиперболический синус является нечетной функцией, возрастающей на всей числовой оси. Гиперболический косинус является четной функцией, убывающей на промежутке (–∞; 0) и возрастающей на промежутке (0; +∞). Точка (0; 1) является минимумом этой функции.
|
|
| График 2.4.5.1. Графики функций y = sh x и y = ch x.
|
По аналогии с тригонометрическими функциями определены гиперболические тангенс и котангенс:
Тангенс определен на всей числовой оси, котангенс – при всех x ≠ 0
(
).
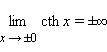Обе функции непрерывны на всей области определения, нечетны и имеют горизонтальные асимптоты y = –1 (при x → –∞) и y = 1 (при x → +∞).
|
|
| График 2.4.5.2. Графики функций y = th x и y = сth x.
|
Приведем некоторые формулы, связанные с гиперболическими функциями.
sh x + ch x = ex
| sh (x + y) = sh x ch y + ch x sh y |
| ch (x + y) = ch x ch y + sh x sh y |
|
Функции, обратные гиперболическим синусу и тангенсу, определены и непрерывны на всей числовой оси. Они обозначаются соответственно arsh x и arth x. У гиперболического косинуса определены сразу две обратные функции: arch– x при x ≤ 0 и arch+ x при x ≥ 0.
|
|
| График 2.4.5.3. Графики функций y = arsh x и y = arth x.
|
|
|
| График 2.4.5.4. Графики функции y = arch– x и y = arch+ x.
|
В заключение приведем формулы для обратных гиперболических функций:
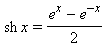
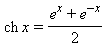
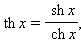
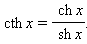
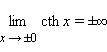