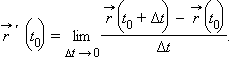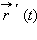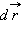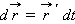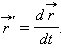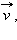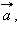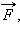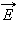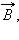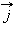Глава 3. Дифференцирование и интегрирование функций
3.1. Производная
3.1.10. Вектор-функции
Пусть каждому значению
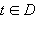 поставлен в соответствие вектор
поставлен в соответствие вектор
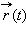 трехмерного пространства. В этом случае говорят, что на множестве D задана векторная функция.
трехмерного пространства. В этом случае говорят, что на множестве D задана векторная функция.
Если в пространстве задана декартова система координат, то задание вектор-функции
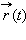 означает задание скалярных функций x (t), y (t), z (t). Если
означает задание скалярных функций x (t), y (t), z (t). Если
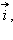
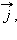
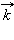 –
единичные векторы координатных осей, то
–
единичные векторы координатных осей, то
Если для любого t начало вектора
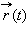 совпадает с началом координат, то говорят о радиус-векторе.
совпадает с началом координат, то говорят о радиус-векторе.
Вектор
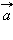 называется пределом вектор-функции
называется пределом вектор-функции
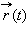 при
при 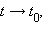 если
если
Пусть

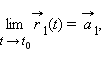
 Тогда
Тогда
Вектор-функцию
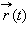 называют непрерывной в точке t0, если
называют непрерывной в точке t0, если
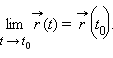
Дифференциалом вектор-функции 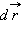 называют линейную вектор-функцию
называют линейную вектор-функцию 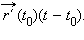 Производная вектор-функции в точке
Производная вектор-функции в точке 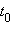 определяется аналогично производной функции одного переменного:
определяется аналогично производной функции одного переменного:
Аналогично вводится понятие второй производной и производных более высоких порядков.
Производная вектор-функции
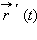 связана с ее дифференциалом
связана с ее дифференциалом
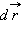 формулой
формулой
или
Вектор-функции широко используются в физике. Так, скорость
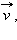 ускорение
ускорение
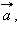 сила
сила
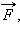 напряженности электрического и магнитного полей
напряженности электрического и магнитного полей
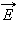 и
и
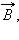 плотность тока
плотность тока
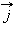 являются векторными функциями координат.
являются векторными функциями координат.






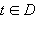
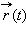
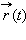
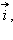
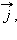
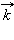 –
–
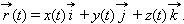
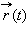
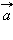
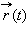
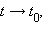 если
если
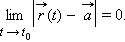

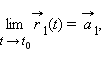

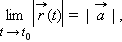
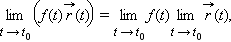
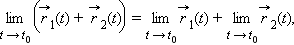
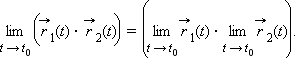
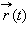
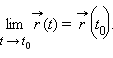
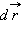 называют линейную вектор-функцию
называют линейную вектор-функцию 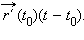 Производная вектор-функции в точке
Производная вектор-функции в точке 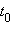 определяется аналогично производной функции одного переменного:
определяется аналогично производной функции одного переменного: