Глава 3. Дифференцирование и интегрирование функций
3.2. Исследование функций при помощи производных
3.2.2. Экстремумы
Напомним, что в точке x0 функция достигает экстремума, если для любых x из некоторой окрестности точки x0 выполняется неравенство f (x) ≤ f (x0) (минимум) или f (x) ≥ f (x0) (максимум).
Теорема Ферма. Если функция f (x) дифференцируема в точке x0 и достигает в ней экстремума, то
|
|
| График 3.2.2.1. Теорема Ферма: касательная к графику функции в точке экстремума параллельна оси абсцисс
|
Необходимое условие экстремума. Во всех точках экстремума производная функции не существует или равна нулю.
Обратное, вообще говоря, неверно. Так, точка x = 0 функции y = x3 не является ни максимумом, ни минимумом.
Точки, в которых производная функции равна нулю, называются стационарными точками функции. Точки, в которых производная функции равна нулю или не существует, называются критическими точками. Таким образом, все экстремумы являются критическими точками
Теорема Ролля. Если функция f (x) непрерывна на отрезке [a; b], принимает в концах этого отрезка равные значения и дифференцируема на интервале (a; b), то существует хотя бы одна точка
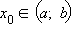 такая, что
такая, что
В частности, между двумя нулями дифференцируемой функции обязательно лежит хотя бы один нуль ее производной.
Теорема Лагранжа. Если функция f (x) непрерывна на отрезке [a; b] и дифференцируема на интервале (a; b), то существует хотя бы одна точка
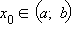 такая, что
такая, что

 |
|
Модель 3.6.
Теорема Лагранжа
|
Это соотношение называется формулой конечных приращений Лагранжа. Воспользовавшись ей, легко доказать, что если производная функции на отрезке [a; b] равна 0, то эта функция постоянна на этом отрезке. Если производная функции f на отрезке [a; b] равна k, то f – линейная функция.
Если в точке x0 функции f и g равны, а производные этих функций, если они существуют, удовлетворяют на некотором отрезке [x0; x1] соотношению f ′ (x) > g′ (x), то в каждой точке промежутка (x0; x1] f (x) > g (x).
Достаточные условия экстремума.
Пусть функция дифференцируема в некоторой окрестности точки x0, кроме, быть может, самой этой точки, и непрерывна в точке x0. Если производная функции меняет знак с минуса на плюс при переходе через эту точку слева направо, то x0 – точка минимума. Если производная функции меняет знак с плюса на минус при переходе через эту точку слева направо, то x0 – точка максимума.
Так, производная функции f (x) = |x| равна –1 при отрицательных x и +1 при положительных x. Функция |x| достигает в точке x0 = 0 своего минимума.
В точке x0 = 0 первая производная функции f (x) = –x2 равна f ′ (x0) = –2x0 = 0, а вторая производная f ′′ (x0) = (–2x)′ = –2 < 0.
Функция –x2 + 3 достигает в точке x0 = 0 своего максимума.
|
|
| График 3.2.2.2. Достаточные условия экстремума
|
|
|
| График 3.2.2.3. Достаточные условия экстремума
|
Заметим, что в точке x = 0 функции y = x4 вторая производная f ′′ (x0) = 0, однако эта точка является точкой минимума. Можно доказать, что если f ′ (x0) = f ′′ (x0) =... = f (2n – 1) (x0) = 0 и f (2n) (x0) > 0 (f (2n) (x0) < 0), то точка x0 является точкой минимума (соответственно, максимума).









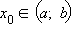
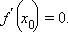

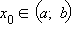
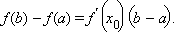




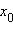 – стационарная точка функции
– стационарная точка функции 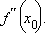
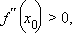
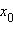 – точка минимума; если
– точка минимума; если
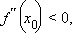
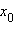 – точка максимума функции
– точка максимума функции 



