Задачи

Решение.

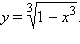
Функция определена на всей числовой оси, пересекает ось абсцисс в точке 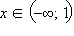x = 1, положительна при и отрицательна при  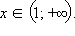 Преобразуя уравнение 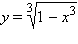к виду  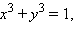 приходим к выводу, что оно симметрично относительно перестановки x и y. Отсюда следует, что график функции симметричен относительно оси y = x.

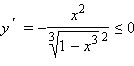при любых x. Функция не имеет экстремумов. При x = 0 график функции имеет горизонтальную касательную, а при x = 1 – вертикальную.

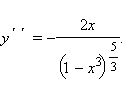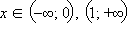  Точки x = 0 и x = 1 являются точками перегиба графика функции. При график функции выпуклый вниз ( 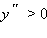), а при 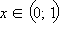– вверх.

Вертикальных асимптот у графика нет. Найдём наклонную асимптоту.

y = –x – асимптота графика.

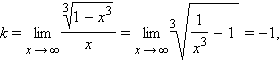
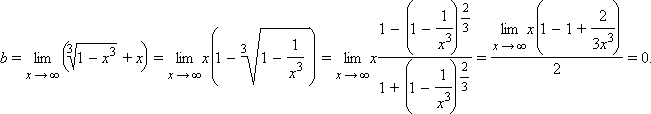
Сведем все данные в таблицу

x	(–∞; 0)	0	(0; 1)	1	(1; +∞)
y	+	1	+	0	–
y′	–	0	–	–∞	–
y′′	+	0	–	±∞	+
Примечание		Точка перегиба		Верт. касат.

График функции показан на рисунке.