Решение.Функция определена на всей числовой оси, пересекает ось абсцисс в точках x = 1, x = 2 и 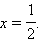 При
При 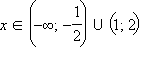 функция положительна, а при
функция положительна, а при 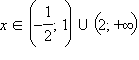 – отрицательна. Асимптот функция не имеет.
– отрицательна. Асимптот функция не имеет.
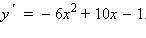 Точка
Точка 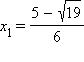 является точкой минимума, а точка
является точкой минимума, а точка 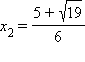 – точкой максимума функции. На промежутках
– точкой максимума функции. На промежутках 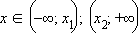 функция убывает, т.к. y′ < 0, а на промежутке
функция убывает, т.к. y′ < 0, а на промежутке 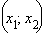 возрастает.
возрастает.
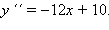 Точка
Точка 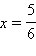 является точкой перегиба функции, причем при
является точкой перегиба функции, причем при 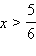 график функции выпуклый вверх (y′′ < 0), а при
график функции выпуклый вверх (y′′ < 0), а при 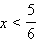 – вниз.
– вниз.
Сведем полученные данные в таблицу.
| x |
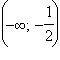 |
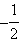 |
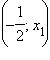 |
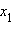 |
 |
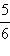 |
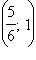 |
1 |
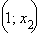 |
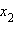 |
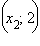 |
2 |
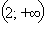 |
| y |
+ |
0 |
– |
≈-2,0 |
– |
 |
– |
0 |
+ |
≈1,0 |
+ |
0 |
– |
| y′ |
– |
– |
– |
0 |
+ |
+ |
+ |
+ |
+ |
0 |
– |
– |
– |
| y′′ |
+ |
+ |
+ |
+ |
+ |
0 |
– |
– |
– |
– |
– |
– |
– |
| Прим. |
|
|
|
Минимум |
|
Точка перегиба |
|
|
|
Максимум |
|
|
|
График функции приведен на рисунке. Уточним его, вычислив несколько дополнительных точек (скажем, x = –1 и x = 3).


 Задачи
Задачи

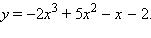
 1 из 7
1 из 7
