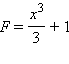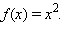Глава 3. Дифференцирование и интегрирование функций
3.3. Неопределенный интеграл
3.3.1. Первообразная
Зная закон движения тела, можно, продифференцировав функцию перемещения тела по времени, в любой момент найти его скорость. Часто требуется решить обратную задачу, то есть найти перемещение тела, зная, как изменяется его скорость. Эта и подобные задачи решаются при помощи интегрирования – операции, обратной дифференцированию.
Функция F, заданная на некотором промежутке D, называется первообразной функции f, заданной на том же промежутке, если для любого
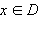
Так, функция
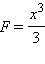 является первообразной функции
является первообразной функции  в чем можно убедиться, поставив эти функции в определение первообразной. Функция
в чем можно убедиться, поставив эти функции в определение первообразной. Функция
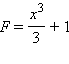 также является первообразной функции
также является первообразной функции 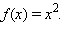
Если функция F является первообразной функции f, то все функции вида F + C, где C – константа, и только они являются первообразными функции f.
Таким образом, для любой функции ее первообразная F определяется неоднозначно. Для того, чтобы задать ее однозначно, нужно указать точку A (x0; y0), удовлетворяющую уравнению y = F (x).

 |
|
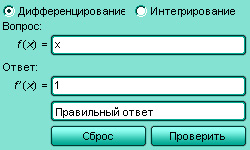
Модель 3.8.
Дифференцирование и интегрирование функций
|
Первообразные основных элементарных функций приведены в таблице.
| Функция f (x) |
Первообразная F (x) |
| 0 |
C |
| a |
xa + C |
| xα, α ≠ –1 |
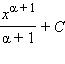 |
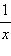 |
ln |x| + C |
| ax |
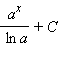 |
| sin x |
–cos x + C |
| cos x |
sin x + C |
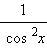 |
tg x + C |
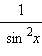 |
–ctg x + C |
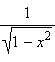 |
arcsin x + C |
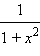 |
arctg x + C |
|
| Таблица 3.3.1.1 |






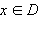
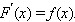
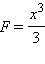
 в чем можно убедиться, поставив эти функции в определение первообразной. Функция
в чем можно убедиться, поставив эти функции в определение первообразной. Функция