Глава 3. Дифференцирование и интегрирование функций

3.3. Неопределенный интеграл

3.3.3. Основные приемы интегрирования

Простейшие задачи, в которых нужно проинтегрировать элементарные функции, решаются при помощи таблицы первообразных. В более сложных случаях нужно знать ряд приемов, сводящих в конечном итоге вычисляемый интеграл к интегралам от табличных функций. Одним из таких приемов является метод замены переменного.

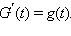
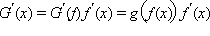
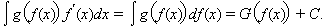Пусть определены дифференцируемые функции f (x) и g (t), а также сложная функция g (f (x)). Пусть Тогда Это означает, что

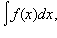
Иногда, вычисляя интеграл 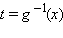полезно перейти к новой переменной. Пусть x = g (t) монотонная дифференцируемая функция, – обратная ей функция. Тогда Обозначая получим f (x) dx = u (t) dt. Если то

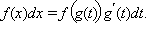
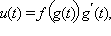
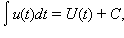
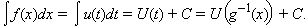Этот метод называется методом подстановки.

Пусть функции u (x) и v (x) имеют непрерывные на D производные. Тогда

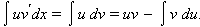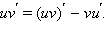
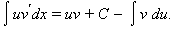
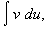
Функция uv имеет непрерывную производную на D, и Интегрируя обе части этого равенства, получим Относя константу интегрирования к интегралу получаем доказываемую формулу.

Эта формула описывает метод интегрирования по частям. Она сводит вычисление интеграла к вычислению интеграла
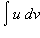
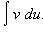