

 |
 |
Данная форма организации контроля знаний, умений и навыков учащихся проводится перед контрольной работой и после самостоятельной работы, когда у учителя уже имеются начальные данные об уровне освоения этой темы каждым учеником, и требуется их откорректировать у одних учащихся и расширить для других.
Блиц-опрос позволяет выявить уровень понимания учениками усвоенного материала. Заслушивая ответы учеников, учитель сможет сделать вывод, кто из учеников имеет:
Вопросы подобраны таким образом, что, используя сочетание словесных и наглядных методов: графиков, рисунков, таблиц, ученик должен не только показать знания основных понятий, но и уметь объяснить их сущность, аргументировать свои суждения, приводить примеры. Учитель же, используя гностические методы, побуждающие к осуществлению мыслительных операций (проблемные вопросы, исследовательские задания), подводит к умению раскрывать элементарные связи между функцией и её первой и второй производными.
При этом используются такие методы, как проблемно-поисковый, когда высказываются предположения о причинах и связях (например, вопрос 10), формулируются выводы, на основе сравнений, рассуждений (например, вопрос 14). При ответе на вопросы № 3, 8, 14 учащимся требуется логически переработать известные понятия, теоремы, обобщить их.
Блиц-опрос проводится при высоком темпе урока. Возможность высказать своё мнение, дополнить ответ предоставляется каждому желающему.
У учащихся на партах в произвольном порядке по одной карточке № 1–16 с вопросами. На карточке с чётным номером вопрос репродуктивного уровня, на карточке с нечётным номером вопрос продуктивного уровня, который может выполняться у доски с приведением краткого решения.
Учитель называет номер вопроса, и ученик сидящий за партой, на которой лежит вопрос с этим номером читает его. Право первым ответить предоставляется ученикам, сидящим за этой партой, затем их ответ может дополнить любой ученик.
Вопросы
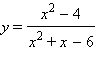
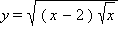
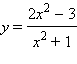
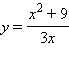
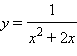
| а) |
в) |
д) |
| б) |
г) |
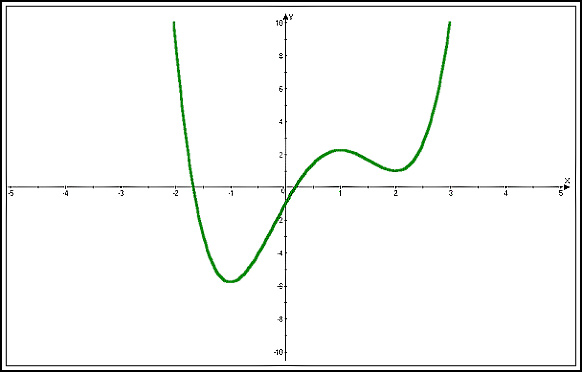
|
| Рисунок M.3.10.1 |
| Монотонно убывает | Имеет максимум во внутренней точке | Имеет минимум во внутренней точке | Постоянна | Монотонно возрастает | |
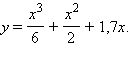
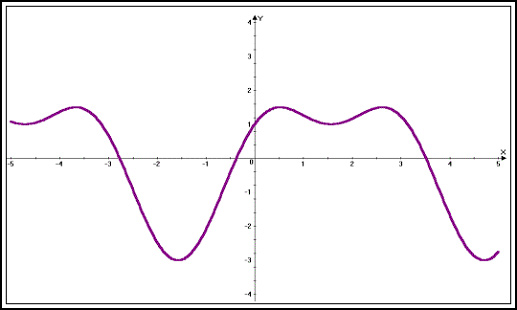
|
| Рисунок M.3.10.2 |
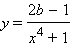 равен 3.
равен 3.
| а) |
в) |
д) |
| б) |
г) |
Рекомендации по оценке знаний при данной форме контроля
Успех данного урока существенно зависит от познавательной активности учащихся, от того, насколько они будут заинтересованы в своей деятельности, потому что ясное знание конкретных целей при условии их посильности, возможность выполнить требования учителя активизирует познавательные способности школьников, причем на разных уровнях. Поэтому для эффективности обучения используются элементы модульной технологии, т.к. при модульном обучении каждый ученик включается в активную и эффективную учебно-познавательную деятельность. Здесь идет индивидуализация контроля, самоконтроля, коррекции, консультирования, степени самостоятельности. Все ответы оцениваются в баллах, результат заносится в таблицу.
Например:
| Фамилия | Ответ по карточке | Дополнение ответа | Общее количество баллов | Оценка ученика | ||||
| Полный ответ с обоснованием (106) | Верный ответ без обоснования (76) | Неполный ответ (1–56) | Формулировка понятия (16) | Формулировка вывода (3–56) | Исправление неточности в ответе другого ученика (1–56) | 106 7–96 4–66 |
«5» «4» «3» |
|
| 1. Астафьев С. | 7 | 5 | 3 | 15 | «5» | |||
 |
 |
 |

