Глава M. Методика

M.3. Методика работы с компьютерным курсом

M.3.11. Коллоквиум. Тема «Функции и графики», 10 класс (профильный уровень)

Место урока

Урок проводится после изучения темы как урок систематизации и контроля знаний. Посвящён повторению, углублению и обобщению пройденного материала. На данном уроке ученики учатся выступать, отстаивать свои суждения, формируют грамотный понятийный аппарат.

Подготовка к коллоквиуму

Учащимся заранее сообщается тема занятия и вопросы, по которым будет проводиться опрос не позднее, чем за две недели до проведения. Указывается литература, распределяются индивидуальные и групповые задания (зависит от уровня подготовленности учеников класса). Ученикам предлагается самим подобрать рациональные способы решения заданий по указанной теме.

Вопросы к коллоквиуму

1. Что такое прямая пропорциональная зависимость между переменными?
2. Что такое обратно пропорциональная зависимость одной переменной от другой?
3. Какой формулой записывается квадратичная зависимость одной переменной от другой?
4. Как называются кривые-графики простейших зависимостей?
5. Приведите несколько примеров прямо пропорциональных величин.
6. Приведите несколько примеров обратно пропорциональных величин.
7. Приведите примеры квадратичной зависимости.
8. Что такое функция?
9. Что такое область определения функции?
10. Что такое график функции?
11. Какие способы задания функции вы знаете?
12. Приведите пример линейной функции.
13. Приведите пример рациональной функции.
14. Приведите пример квадратичной функции.
15. Приведите пример функции, область определения которой меньше, чем вся числовая ось.
16. Приведите пример графического задания функции.
17. Как с помощью графика найти область определения функции?
18. Как с помощью графика найти нули функции?
19. Как с помощью графика найти промежутки знакопостоянства?
20. Что такое точка локального максимума (минимума) функции?
21. Как найти промежутки возрастания (убывания) функции?
22. Чем отличается наибольшее значение функции от её локального максимума?
23. Как по графику найти область значений функции?
24. Как графически решается уравнение вида f (x) = g (x)?
25. Как графически решается неравенство вида f (x) > g (x)?
26. Перечислите, какие характеристики функции включаются в схему её исследования.
27. Перечислите свойства линейной функции.
28. Можно ли сказать, что линейная функция является монотонной на всей числовой оси? От чего зависит характер монотонности линейной функции?
29. Сколько раз меняет знак линейная функция? Как определить точку, в которой линейная функция меняет знак?
30. Какие значения может принимать линейная функция?
31. Каких данных достаточно для того, чтобы построить график линейной функции?
32. Как вычислить угловой коэффициент прямой, если известны две её точки?
33. Как будет перемещаться график функции y = f (x – a) при изменении параметра а?
34. Как будет перемещаться график функции y = f (x) + b при изменении параметра b?
35. Как связаны между собой графики функций y = f (x), y = f (–x), y = –f (x)?
36. Как связаны между собой области определения функций y = f (x), y = f (–x), y = –f (x), y = f (x – a), y = f (x + b)?
37. Как будет меняться график функции y = f (kx) при изменении параметра k? Тот же вопрос для функции y = kf (x).
38. Как построить график произвольной дробно-рациональной функции ?
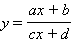39. Как вычислить координаты вершины параболы, от чего зависит, будут ли ветви параболы направлены вверх или вниз?
40. Что такое непрерывная функция?
41. Приведите примеры разрывных функций.
42. Операции над функциями: сумма, произведение. Приведите примеры.
43. Композиция функций, как найти её область определения?
44. Возрастание и убывание функций.
45. Свойства композиций функций.
46. Ограниченные и неограниченные функции.
47. Построение графиков, содержащих модуль.
48. Предел функции на бесконечности.
49. Предел функции в точке.
50. Окрестность точки, проколотая окрестность точки.
51. Горизонтальная асимптота.
52. Вертикальная асимптота.
53. Наклонная асимптота.
54. Теорема о промежуточном значении функции, непрерывной на отрезке.
55. Метод интервалов.

Коллоквиум проходит «за круглым столом». Перед учениками вопросы к коллоквиуму. Учитель зачитывает вопрос, по желанию отвечает любой ученик, даёт по мере возможности наиболее полный ответ. Затем другие ученики дополняют, высказывают свои замечания, несогласия с формулировками. Получив полный ответ, переходят к другому вопросу. Учитель фиксирует ответы учащихся, дополнения к ответам в таблице, по окончании выставляется оценки. С целью стимулирования ответов, предлагается учеников, получивших положительную оценку, освободить от выполнения контрольной работы.
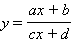