Глава 2. Электромагнитные колебания и волны

2.3. Вынужденные колебания. Переменный ток

Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями.

Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Внешний источник периодического воздействия обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.

Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте ω₀.

Если частота ω₀ свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте ω внешнего источника.

Для установления вынужденных стационарных колебаний после включения в цепь внешнего источника необходимо некоторое время Δt. Это время по порядку величины равно времени τ затухания свободных колебаний в цепи.

Электрические цепи, в которых происходят установившиеся вынужденные колебания под действием периодического источника тока, называются цепями переменного тока.

Рассмотрим последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рис. 2.3.1):

e (t) = 0 cos ωt,

где ₀ – амплитуда, ω – круговая частота.

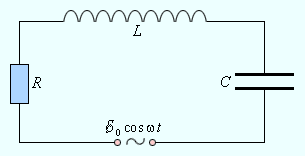
Рисунок 2.3.1. Вынужденные колебания в контуре

Предполагается, что для электрической цепи, изображенной на рис. 2.3.1, выполнено условие квазистационарности. Поэтому для мгновенных значений токов и напряжений можно записать закон Ома:

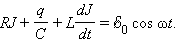Величина 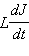– это ЭДС самоиндукции катушки, перенесенная с изменением знака из правой части уравнения в левую. Эту величину принято называть напряжением на катушке индуктивности.

Уравнение вынужденных колебаний можно записать в виде

uR + uC + uL = e (t) = 0 cos ωt,

где u_R (t), u_C (t) и u_L (t) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами U_R, U_C и U_L. При установившихся вынужденных колебаниях все напряжения изменяются с частотой ω внешнего источника переменного тока. Для наглядного решения уравнения вынужденных колебаний можно использовать метод векторных диаграмм.

На векторной диаграмме колебания определенной заданной частоты ω изображаются с помощью векторов (рис. 2.3.2).

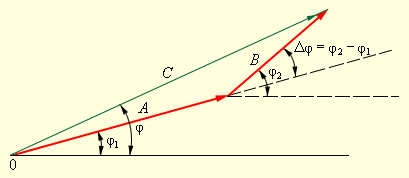
Рисунок 2.3.2. Изображение гармонических колебаний A cos (ωt + φ1), B cos (ωt + φ2) и их суммы C cos (ωt + φ) с помощью векторов на векторной диаграмме

Длины векторов на диаграмме равны амплитудам 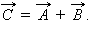A и B колебаний, а наклон к горизонтальной оси определяется фазами колебаний φ₁ и φ₂. Взаимная ориентация векторов определяется относительным фазовым сдвигом Δφ = φ₁ – φ₂. Вектор, изображающий суммарное колебание, строится на векторной диаграмме по правилу сложения векторов:

Для того, чтобы построить векторную диаграмму напряжений и токов при вынужденных колебаниях в электрической цепи, нужно знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для всех участков цепи.

Рассмотрим по отдельности случаи подключения внешнего источника переменного тока к резистру с сопротивлением R, конденсатору с емкостью C и катушки с индуктивностью L. Во всех трех случаях напряжение на резисторе, конденсаторе и катушке равно напряжению источника переменного тока.

1. Резистор в цепи переменного тока

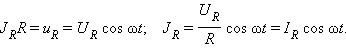Здесь через I_R обозначена амплитуда тока, протекающего через резистор. Связь между амплитудами тока и напряжения на резисторе выражается соотношением

RIR = UR.

Фазовый сдвиг между током и напряжением на резисторе равен нулю.

Физическая величина R называется активным сопротивлением резистора.

2. Конденсатор в цепи переменного тока

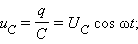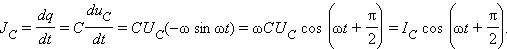Соотношение между амплитудами тока I_C и напряжения U_C:

Ток опережает по фазе напряжение на угол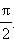

Физическая величина 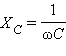называется емкостным сопротивлением конденсатора.

3. Катушка в цепи переменного тока

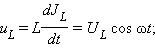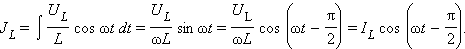Соотношение между амплитудами тока I_L и напряжения U_L:

ω L IL = UL.

Ток отстает по фазе от напряжения на угол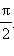

Физическая величина X_L = ωL называется индуктивным сопротивлением катушки.

Теперь можно построить векторную диаграмму для последовательного RLC-контура, в котором происходят вынужденные колебания на частоте ω. Поскольку ток, протекающий через последовательно соединенные участки цепи, один и тот же, векторную диаграмму удобно строить относительно вектора, изображающего колебания тока в цепи. Амплитуду тока обозначим через I₀. Фаза тока принимается равной нулю. Это вполне допустимо, так как физический интерес представляют не абсолютные значения фаз, а относительные фазовые сдвиги. Векторная диаграмма для последовательного RLC-контура изображена на рис. 2.3.2.

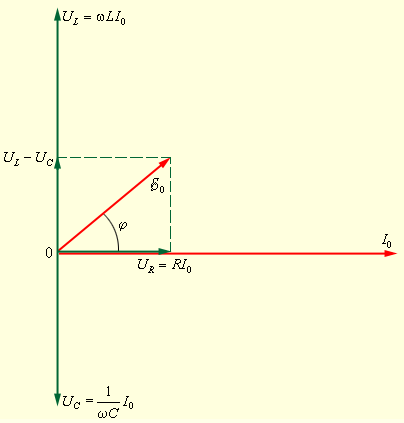
Рисунок 2.3.3. Векторная диаграмма для последовательной RLC-цепи

Векторная диаграмма на рис. 2.3.2 построена для случая, когда 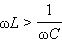или 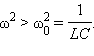В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.

Из рисунка видно, что
откуда следует

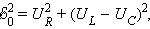Из выражения для I₀ видно, что амплитуда тока принимает максимальное значение при условии
или

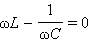Явление возрастания амплитуды колебаний тока при совпадении частоты ω колебаний внешнего источника с собственной частотой ω₀ электрической цепи называется электрическим резонансом. При резонансе

Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).

При последовательном резонансе (ω = ω₀) амплитуды U_C и U_L напряжений на конденсаторе и катушке резко возрастают:

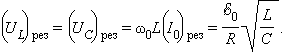В § 2.2 было введено понятие добротности RLC-контура:

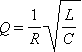Таким образом, при резонансе амплитуды напряжений на конденсаторе и катушке в Q раз превышают амплитуду напряжения внешнего источника.

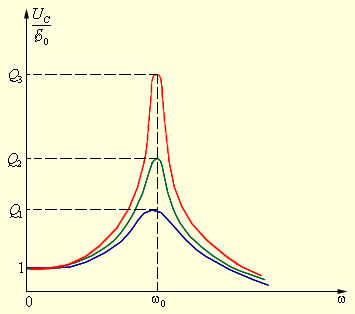
Рисунок 2.3.4. Резонансные кривые для контуров с различными значениями добротности Q

Рис. 2.3.4 иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды U_C напряжения на конденсаторе к амплитуде ₀ напряжения источника от его частоты ω для различных значений добротности Q. Кривые на рис. 2.3.3 называются резонансными кривыми.

Можно показать, что максимум резонансных кривых для контуров с низкой добротностью несколько сдвинуты в область низких частот.

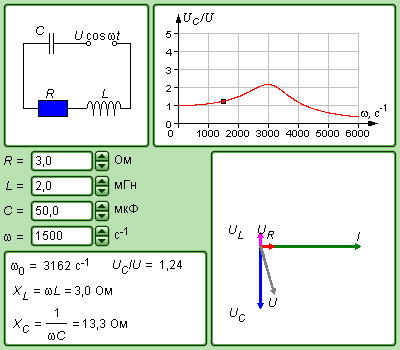Модель. Вынужденные колебания в RLC-контуре