Глава 3. Оптика

Волновая оптика

3.9. Дифракционный предел разрешения оптических инструментов

Для практики наиболее интересен случай дифракции света, когда препятствие оставляет открытой лишь малую часть 1-й зоны Френеля. Этот случай реализуется при условии
т. е. дифракционную картину от препятствий небольшого размера следует в этом случае наблюдать на очень больших расстояниях. Например, если R = 1 мм, λ = 550 нм (зеленый свет), то расстояние L до плоскости наблюдения должно быть значительно больше 2 метров (т. е. минимум 10 метров или больше). Лучи проведенные в далекую точку наблюдения от различных элементов волнового фронта, практически можно считать параллельными. Этот случай дифракции так и называется – дифракция в параллельных лучах или дифракция Фраунгофера – по имени немецкого физика И. Фраунгофера, современника Френеля. Если на пути лучей за препятствием поставить собирающую линзу, то параллельный пучок лучей, дифрагировавший на препятствии под углом θ, соберется в некоторой точке фокальной плоскости (рис. 3.9.1). Следовательно, любая точка в фокальной плоскости линзы эквивалентна бесконечно удаленной точке в отсутствие линзы.

Рисунок 3.9.1. Дифракция в параллельных лучах. Зеленая кривая – распределение интенсивности в фокальной плоскости (масштаб по оси x сильно увеличен)

В фокальной плоскости линзы наблюдается дифракционная картина Фраунгофера. Но, согласно геометрической оптике, в фокусе линзы должно располагаться точечное изображение удаленного точечного предмета. На самом деле изображение точечного предмета оказывается размытым из-за дифракции. В этом проявляется волновая природа света.

Никакая оптическая система не может дать точечного изображения. В случае дифракции Фраунгофера на круглом отверстии диаметра D дифракционное изображение состоит из центрального светлого пятна (диск Эйри), на которое приходится приблизительно 85 % энергии света, и окружающих его светлых и темных колец (рис. 3.9.2). Это дифракционное пятно и принимается за изображение точечного источника. Радиус центрального пятна в фокальной плоскости линзы равен

Если лучи света от удаленного источника падают на линзу непосредственно, то роль экрана, на котором дифрагирует свет, выполняет оправа линзы. В этом случае под D нужно понимать диаметр линзы.

Рисунок 3.9.2. Дифракционное изображение точечного источника (дифракция на круглом отверстии). В центральное пятно попадает приблизительно 85 % энергии света

Размер дифракционных изображений очень мал. Например, радиус центрального светлого пятна в фокальной плоскости линзы диаметром D = 5 см с фокусным расстоянием F = 50 см в монохроматическом свете с длиной волны λ = 500 нм приблизительно равен 0,006 мм. Во многих оптических устройствах (фотоаппараты, проекторы и т. д.) дифракционное размытие изображений маскируется значительно более сильными искажениями из-за несовершенства оптики. Но в высокоточных астрономических приборах реализуется дифракционный предел качества изображений. Вследствие дифракционного размытия изображения двух близких точек объекта могут оказаться неотличимы от изображения одной точки. Рассмотрим в качестве примера объектив астрономического телескопа, нацеленного на две близкие звезды, находящиеся на угловом расстоянии ψ друг от друга. Предполагается, что все дефекты и аберрации устранены, и в фокальной плоскости объектива наблюдаются дифракционные изображения звезд (рис. 3.9.3).

Рисунок 3.9.3. Дифракционные изображения двух близких звезд в фокальной плоскости объектива телескопа

На рис. 3.9.3 расстояние Δl между центрами дифракционных изображений звезд превышает радиус r центрального светлого пятна – в этом случае изображения звезд воспринимаются наблюдателем раздельно и, следовательно, объектив телескопа позволяет разрешить две близкие звезды. При уменьшении углового расстояния ψ между звездами дифракционные изображения могут сильно перекрыться и перестанут отличаться от изображения одиночной звезды. В этом случае объектив телескопа не разрешает близкие звезды. Английский физик Дж. Релей в конце XIX в. предложил условно считать разрешение полным, когда расстояния Δl между центрами изображений равно (или превышает) радиус r диска Эйри (рис. 3.9.4). Условие Δl = r называют критерием разрешения Релея. Из этого критерия следует:

Телескоп с диаметром объектива D = 1 м способен разрешать две звезды, находящиеся на угловом расстоянии ψ_min = 6,7·10^–7 рад (для λ = 550 нм).

Рисунок 3.9.4. Предел разрешения по Релею. Красная кривая – распределение суммарной интенсивности света

Космический телескоп Хаббла, выведенный на орбиту в 1990 году, имеет зеркало диаметром D = 2,40 м. Предельное угловое разрешение этого телескопа на длине волны λ = 550 нм равно: ψ_min = 2,8·10^–7 рад. На работу космического телескопа не оказывают влияния атмосферные возмущения. Для характеристики объектива телескопа можно ввести величину R, обратную предельному углу ψ_min. Эту величину называют разрешающей силой телескопа:

Для увеличения разрешающей способности телескопа следует увеличивать диаметр объектива (либо переходить к более коротким волнам). Все сказанное выше о разрешающей способности телескопа применимо и к невооруженному глазу. Глаз при рассматривании удаленных предметов действует так же, как и объектив телескопа. Роль D играет диаметр зрачка глаза d_зр. Полагая d_зр = 3 мм, λ = 550 нм, найдем для предельного углового разрешения глаза

Этот результат хорошо согласуется с физиологической оценкой разрешающей способности глаза, выполненной исходя из размеров светочувствительных элементов сетчатки (палочек и колбочек).

Теперь можно сделать один общий вывод: световой пучок с диаметром D и длиной волны λ вследствие волновой природы света испытывает дифракционное уширение. Угловая полуширина φ пучка оказывается порядка λ / D, так что полная ширина d пучка на расстоянии L приблизительно равна

Рис. 3.9.5 качественно показывает, как по мере удаления от препятствия трансформируется пучок света.

Рисунок 3.9.5. Пучок света, расширяющийся вследствие дифракции. Область I – понятие луча света, законы геометрической оптики. Область II – зоны Френеля, пятно Пуассона. Область III – дифракция в параллельных лучах

Оценки, выполненные на рис. 3.9.5, показывают, что угловое расхождение пучка уменьшается при увеличении его первоначального поперечного размера D. Этот вывод справедлив для волн любой физической природы. Чтобы, например, послать «узкий» пучок лазерного излучения на Луну, нужно сначала его расширить. Это достигается с помощью телескопа: лазерный пучок направляется в окуляр и затем, пройдя через телескоп, выходит из объектива, имея диаметр D (рис. 3.9.6).

Рисунок 3.9.6. Расширение лазерного пучка с помощью телескопической системы

Такой расширенный пучок, дойдя до Луны, «засветит» на ее поверхности пятно радиусом где L – расстояние до Луны. Приняв D = 2,5 м (телескоп-рефлектор Крымской обсерватории), λ = 550 нм, L = 4·10⁶ м, получим R ≈ 90 м. Если бы на Луну был направлен первоначальный пучок лазерного света, имеющий диаметр порядка 1 см, то он «засветил» бы на Луне пятно, радиус которого оказался бы в 250 раз больше.

Разрешающая способность микроскопа. С помощью микроскопа наблюдают близко расположенные объекты, поэтому его разрешающая способность характеризуется не угловым, а линейным расстоянием между двумя близкими точками, которые еще могут восприниматься раздельно. Наблюдаемый объект располагается вблизи переднего фокуса объектива. Часто пространство перед объективом заполняется специальной прозрачной жидкостью – иммерсией (рис. 3.9.7). В плоскости, геометрически сопряженной объекту, располагается его увеличенное изображение, которое рассматривается глазом через окуляр. Изображение каждой точки оказывается размытым вследствие дифракции света.

Рисунок 3.9.7. Иммерсионная жидкость перед объективом микроскопа

Впервые предел разрешения объектива микроскопа был определен в 1874 г. немецким физиком Г. Гельмгольцем. Формула Гельмгольца имеет вид:

Здесь λ – длина волны, n – показатель преломления иммерсионной жидкости, α – так называемый апертурный угол (рис. 3.9.7). Величина n sin α называется числовой апертурой.

У хороших микроскопов апертурный угол α близок к своему пределу: α ≈ π / 2. Как видно из формулы Гельмгольца, применение иммерсии несколько улучшает предел разрешения. Полагая для оценок sin α ≈ 1, n ≈ 1,5, получим:

l_min ≈ 0,4 λ.

Таким образом, с помощью микроскопа принципиально невозможно рассмотреть какие-либо детали, размер которых значительно меньше длины волны света. Волновые свойства света определяют предел качества изображения объекта, полученного с помощью любой оптической системы.

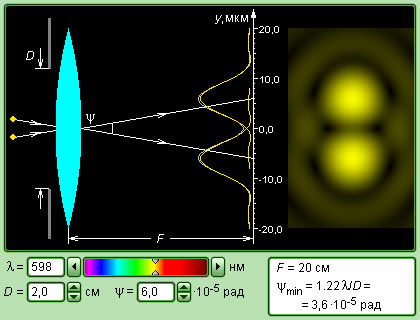
Модель. Дифракционный предел разрешения