Задачи с решениями

Шаг 1

На чертеже изображена трапеция ABCD, вписанная в нее окружность с центром в точке O и заданные отрезки.

Шаг 2

Центр вписанной окружности лежит на пересечении биссектрис углов трапеции. CO – биссектриса угла C, DO – биссектриса угла D, Поскольку BCD + ADC = 180°, OCD + ODC = 90°, значит, COD = 90°.

Шаг 3

Из прямоугольного треугольника ΔCOD по теореме Пифагора имеем:

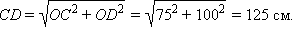
Шаг 4

Проведем радиусы окружности из точек ее касания с трапецией: OM = ON = OP = OQ = r. Из прямоугольного треугольника ΔCOD имеем: r · CD = CO · DO или r · 125 = 75·100, откуда r = 60 см.

Шаг 5

Треугольник ΔAOB – прямоугольный, поскольку AO и BO – биссектрисы углов ABC и BAD, сумма которых равна 180°.

Шаг 6

Из прямоугольного треугольника ΔPOB имеем: 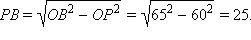  Из прямоугольного треугольника ΔAOB имеем: OP² = PB · PA или 60² = 25 · PA, откуда PA = 144 см. Значит, BA = BP + PA = 25 + 144 = 169 см.

Шаг 7

Сумма боковых сторон трапеции равна AB + DC = 169 + 125 = 294 см. Поскольку трапеция описанная, то BC + AD = AB + DC = 294 см. Таким образом, периметр трапеции равен AB + BC + CD + DA = 2·294 = 588 см.