

 |
 |
Рассмотрим некоторое множество
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
Аналогично определяется пересечение и объединение любого числа множеств.
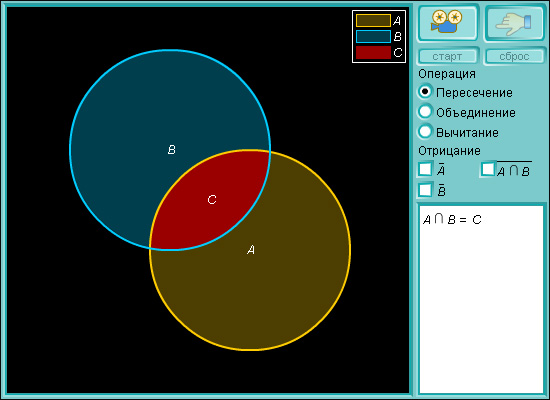
Для удобства множества изображают в виде кругов, а основное множество в виде прямоугольника, их содержащего. Такие рисунки называются диаграммами Эйлера–Венна.

 |
|
Модель 4.1.
Множества на плоскости
|
Пусть 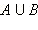 и
и 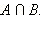
Операции объединения и пересечения множеств обладают следующими свойствами. |
Если |
Например, 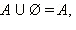
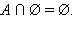
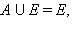
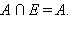
Следует заметить, что мощность объединения и пересечения двух конечных множеств связаны следующим соотношением:
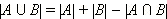 |
Для бесконечных множеств это равенство неверно. Если хотя бы одно из множеств 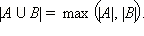
Пусть теперь
 |
 |
|
 |
 |
|
Кратко это можно записать так:
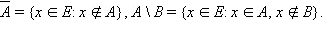
Очевидно, что 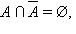
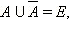
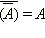 для любого
для любого 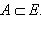
Пусть
Законы де Моргана можно проиллюстрировать при помощи диаграмм Эйлера–Венна.
 |
 |
 |

