

 |
 |
Тема. Формулы сокращённого умножения.
Цель урока. Научиться использовать на практике формулы сокращённого умножения при решении задач.
Основные понятия. Формулы сокращённого умножения: квадрат суммы, квадрат разности, разность квадратов, сумма кубов, разность кубов.
Самостоятельная деятельность учащихся. Применение формул сокращённого умножения при решении задач.
План урока
| Этапы урока | Время, мин | Приемы и методы |
| I. Этап актуализации знаний. Мотивация учебной проблемы | 2 | Беседа учителя |
| II. Основное содержание урока. Формирование у учащихся представления о формулах сокращенного умножения | 10 | Объяснение учителя. Эвристическая беседа |
| III. Формирование умений и навыков. Отработка изученного материала | 25 | Решение задач. Ответы на вопросы учащихся |
| IV. Первичная проверка усвоения знаний. Рефлексия | 5 | Сообщение учителя. Сообщения учащихся |
| V. Домашнее задание | 3 | Запись на доске |
Методический комментарий учителю
Эта тема является основополагающей в разделе «Тождественные преобразования алгебраических выражений». Поэтому важно чтобы учащиеся автоматически умели не только видеть в примерах формулы сокращённого умножения, но и применять их в других заданиях: в таких как решение уравнений, преобразование выражений, доказательство тождеств. Приведём такую подборку упражнений, с помощью которых, на наш взгляд, удобно отработать на практике формулы сокращённого умножения. Обращаем ваше внимание, что упражнения идут по линии нарастания трудности материала (от простого к сложному). Эта подборка задач поможет правильно оценить и сильных, и слабых учеников.
Основное содержание урока
Раскройте скобки:
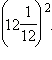
Выполните умножение:
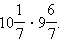
Выполните умножение:
Преобразуйте в многочлен стандартного вида:
Решите уравнение
 |
 |
 |

