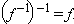Глава 12. Преобразования
12.1. Основные понятия и свойства
В задачах, изучаемых в курсе геометрии, важное значение имеет понятие равенства фигур. Это понятие было ранее определено для простейших фигур: треугольник, окружность, многоугольник и т. д. Для более сложных фигур понятие их равенства дается на основе понятия преобразования фигур.
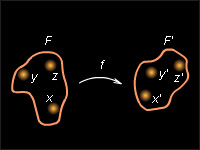
Пусть задана фигура F, и каждой ее точке сопоставлена (ставится в соответствие) единственная точка плоскости. Множество точек, сопоставленных точкам фигуры F, является некоторой фигурой F', вообще говоря, отличной от фигуры F (см. рис. 12.1.1).
Говорят, что фигура F' получена преобразованием фигуры F. Можно также сказать, что фигура F' является образом фигуры F при данном преобразовании. Фигуру F называют прообразом фигуры F'.
Если под F' понимается вся плоскость, можно отвлечься от понятия фигуры и говорить о преобразовании просто точек плоскости. При этом говорят, что задано преобразование на плоскости, если любой точке плоскости ставится в соответствие единственная точка плоскости. При этом если A – точка плоскости, которой сопоставлена точка A1, то A1 – образ точки A, а A – прообраз точки A1.
 1
|
| Рисунок 12.1.1. Преобразование фигур
|
Два преобразования f и g называются равными (совпадают), если для любой точки X, образы ее при преобразованиях f и g совпадают, т.е. f (X) = g (X). Результирующее преобразование h двух последовательно выполненных преобразований f и g фигуры F называется композицией (или суперпозицией) преобразований f и g и записывается h = g ○ f.
 2
|
| Рисунок 12.1.2. Композиция преобразований
|
Неподвижной точкой преобразования f называется такая точка A, что 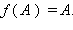 Тождественным называется преобразование, все точки которого неподвижны; оно обозначается буквой e. Преобразование называется взаимно однозначным, если разным точкам фигуры F соответствуют разные образы. Пусть f – взаимно однозначное преобразование, ставящее в соответствие точке X точку X', т. е.
Тождественным называется преобразование, все точки которого неподвижны; оно обозначается буквой e. Преобразование называется взаимно однозначным, если разным точкам фигуры F соответствуют разные образы. Пусть f – взаимно однозначное преобразование, ставящее в соответствие точке X точку X', т. е.
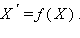 Преобразование
Преобразование
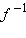 называется обратным к f, если образом точки
называется обратным к f, если образом точки 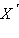 является точка X – прообраз точки
является точка X – прообраз точки
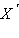 при преобразовании f. Преобразование, обратное к преобразованию
при преобразовании f. Преобразование, обратное к преобразованию 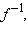 равно f:
равно f:








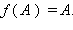 Тождественным называется преобразование, все точки которого неподвижны; оно обозначается буквой
Тождественным называется преобразование, все точки которого неподвижны; оно обозначается буквой 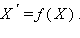 Преобразование
Преобразование
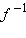 называется обратным к
называется обратным к 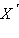 является точка
является точка 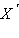 при преобразовании
при преобразовании 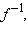 равно
равно