Глава 3. Дифференцирование и интегрирование функций
3.1. Производная
3.1.8. Линеаризация элементарных функций
Рассмотрим функции y = sin x и y = x в окрестности точки x = 0. Увеличивая масштаб графика, можно убедиться, что sin x ≈ x при x → 0. Более точное приближение дает
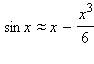 при x → 0. Добавляя в эту формулу все более и более высокие степени x с определенными коэффициентами, мы будет получать все более и более точное представление функции sin x многочленом. Такой многочлен называют многочленом Тейлора.
при x → 0. Добавляя в эту формулу все более и более высокие степени x с определенными коэффициентами, мы будет получать все более и более точное представление функции sin x многочленом. Такой многочлен называют многочленом Тейлора.
|
|
| График 3.1.8.1. Функции y = x3 – 3x и y = –3x2 – 6x – 1 очень «похожи» в окрестности точки x = –1. |
В общем случае функция f (x) представляется в бесконечно малой окрестности точки x0 многочленом Тейлора, задаваемым формулой
где o ((x – x0)n) – бесконечно малая относительно (x – x0)n функция. Естественно, данная формула справедлива, если в точке x0 существуют производные функции f вплоть до f (n). Напомним, что операция факториал определяется следующим образом:
| n! = 1 · 2 · 3 ·…· (n – 1) · n, |
| (2n)!! = 2 · 4 ·…· (2n – 2) · 2n, |
| (2n + 1)!! = 1 · 3 ·…· (2n – 1) · (2n + 1), |
В окрестности x = 0 формула Тейлора приобретает вид
Эта формула называется формулой Маклорена.

 |
|
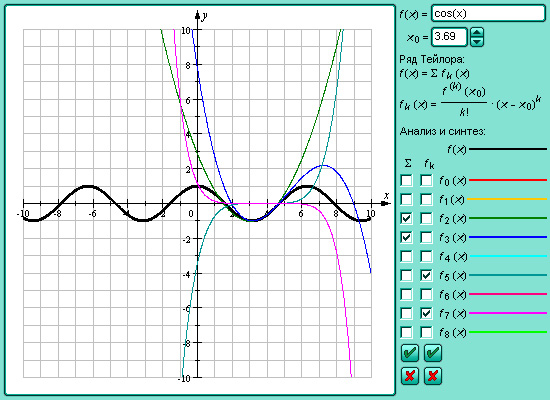
Модель 3.5.
Линеаризация функций
|
Приведем формулы разложения по степеням x некоторых элементарных функций при x → 0.
Формулы Тейлора и Маклорена используются при приближенных вычислениях и для нахождения пределов функций. В частности, ряд Тейлора применяется для вычисления пределов вида
где f (x) > 0, 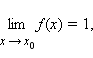
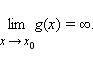 Если
Если 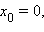
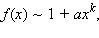
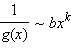 при x → 0, где a ≠ 0, b ≠ 0,
при x → 0, где a ≠ 0, b ≠ 0, 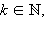 то
то 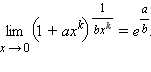 Если
Если 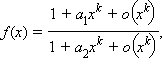
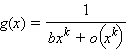 при x → 0, причем
при x → 0, причем 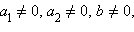 то
то
Если 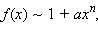
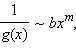 где
где 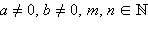 то
то
при n > m.
если m > n и m – n – четное число. Если же m > n и m – n – нечетное число, то 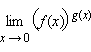 не существует.
не существует.






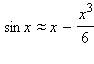
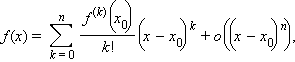
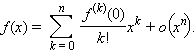


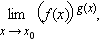
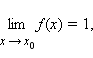
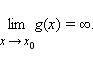 Если
Если 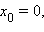
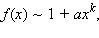
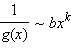 при
при 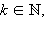 то
то 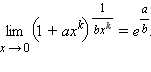 Если
Если 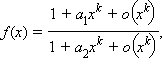
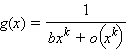 при
при 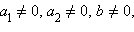 то
то
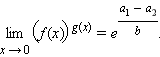
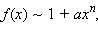
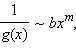 где
где 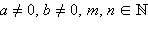 то
то
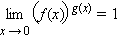
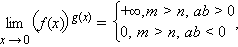
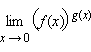 не существует.
не существует.




