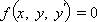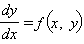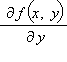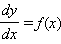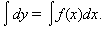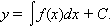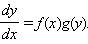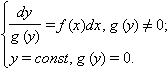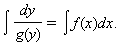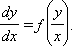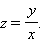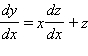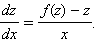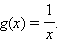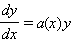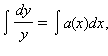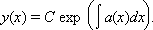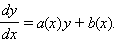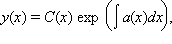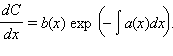Глава 3. Дифференцирование и интегрирование функций

3.5. Простейшие дифференциальные уравнения

3.5.2. Дифференциальные уравнения первого порядка

Уравнение вида
называется обыкновенным дифференциальным уравнением первого порядка. Рассмотрим способы решения некоторых его типов.

Для уравнений вида
с заданными граничными условиями доказана теорема существования и единственности.

Пусть в области D плоскости (x, y) функция f (x, y) и ее частная производная 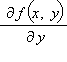непрерывны. Тогда через каждую точку (x₀; y₀) этой области проходит одна и только одна интегральная кривая.

1. Автономное уравнение

Домножим обе части уравнения на dx и проинтегрируем обе части получившегося уравнения: 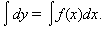Таким образом,

2. Уравнение с разделяющимися переменными

Это уравнение сводится к системе 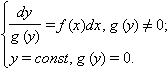В первом уравнении после интегрирования находим y как неявную функцию от x:

3. Однородное уравнение

Пусть 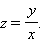Тогда y = zx 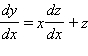и и

Задача сводится к решению уравнения с разделяющимися переменными, где F(x) = f(x) – z,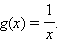

4. Линейное однородное уравнение
является уравнением с разделяющимися переменными и интегрируется по частям: 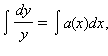откуда

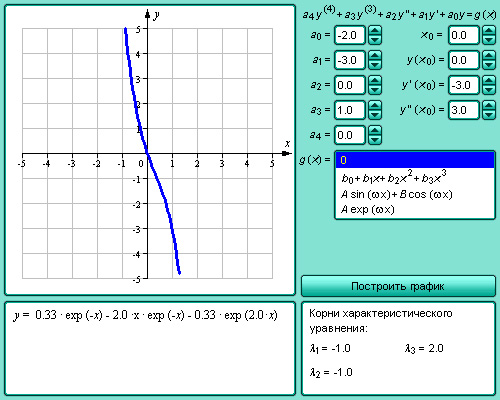
Модель 3.17. Линейные дифференциальные уравнения

5. Линейное уравнение

Будем искать решение этого уравнения в виде 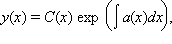где C (x) – неизвестная функция. Тогда 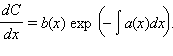Вычисляя отсюда C (x) и подставляя эту функцию в предыдущее равенство, находим решение y (x).